技术中心

偏振光学基础知识（一）：理解偏振光

发布时间：2020-05-13 16:10:02 阅读次数：228

光可以看作是一种横电磁波，它具有相互耦合的电场分量和磁场分量。我们通常考虑的光的偏振特性，是指光波的电矢量大小和方向的变化规律，也就是说，光矢量（一般指电场分量）的大小和方向呈规律变化的光波称为偏振光。

根据光的偏振特性，可以将光波分为自然光、部分偏振光和偏振光，其中偏振光又分为线偏振光、圆偏振光、椭圆偏振光及矢量偏振光。

→ 自然光：光源各原子辐射体所发出的各个波列的振动方向和相位是随机的，同一原子在不同时刻发出的波列，其振动方向和相位也是随机的，因此在观测时间T内（T≫波列存在的时间），总的振动在各个方向上完全平均，这种光被称为自然光。如图1，它包括了垂直于光波传播方向（图中红点所示方向）的所有可能的振动方向。

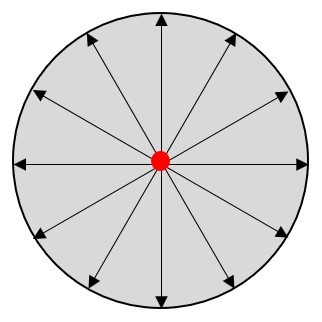
图1.自然光。

→ 偏振光：根据光矢量的大小和方向的变化规律，偏振光可以分为线偏振光、圆偏振光、椭圆偏振光和矢量偏振光。如图2a、2b、2c，分别表示了线偏振光、圆偏振光和椭圆偏振光，其中圆点表示光传播方向。

☆线偏振光在传播过程中，光矢量的方向保持不变，其大小随相位变化，在垂直于光传播方向的平面上，光矢量端点的轨迹是一条直线。

☆圆偏振光在传播过程中，光矢量的大小不变，方向呈规则变化，在垂直于光传播方向的平面上，光矢量端点的轨迹是一个正圆。

☆椭圆偏振光的光矢量大小和方向在传播过程中均呈规则变化，在垂直于光传播方向的平面上，光矢量端点的轨迹是一个椭圆。

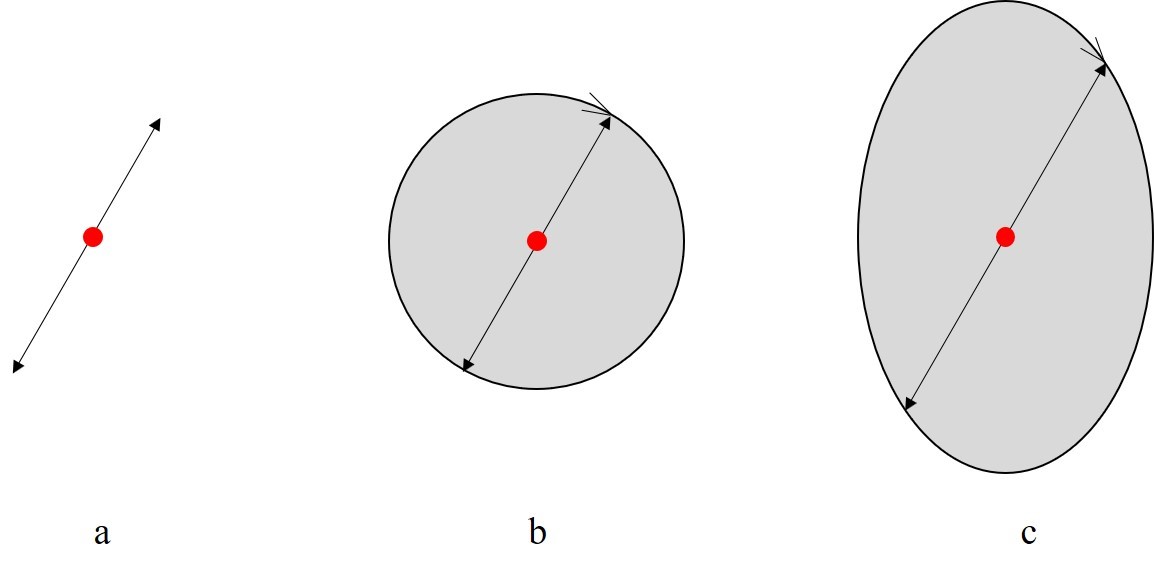
图2.偏振光。

需要指出的是，不管是线偏振光、圆偏振光还是椭圆偏振光，它们在光束横截面上的不同位置，都具有相同偏振态分布，被统一称为标量偏振光束。与之对应的，还有一种矢量偏振光束，矢量偏振光束在光束横截面上不同位置的偏振态呈现非均匀分布，其中最为特殊的一种矢量偏振光束就是偏振态在光束横截面上呈轴对称分布的柱矢量偏振光束，最典型的两类柱矢量偏振光束分别为光束横截面上偏振沿半径方向的径向偏振光束和沿方位角方向的方位角偏振光束。矢量偏振光束是一种近年来才发展成熟的新型光束，如果没有特殊说明，一般所述偏振光指的是标量偏振光束，即线偏振光、圆偏振光和椭圆偏振光。

→ 部分偏振光：通常不管是天然光源还是人造光源，既不是纯粹的自然光，也不是完全的偏振光，这样的光叫做部分偏振光。部分偏振光可以看作是一定比例的自然光和线偏振光线性叠加的结果，它在某些方向上的振动比其他方向占优势。可以定义偏振度P来描述光的偏振程度：

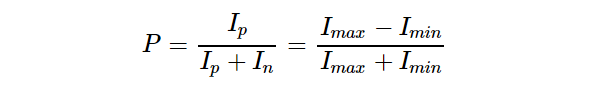
式中，\( I_p \) 表示完全偏振光的光强度，\( I_n \) 表示自然光的光强度，\( I_{max} \) 表示光矢量中占据优势的振动方向的光强度，\( I_{min} \) 表示光矢量中处于劣势的振动方向的光强度。显然，自然光的偏振度P=0，完全线偏振光P=1，部分偏振光0<P<1。

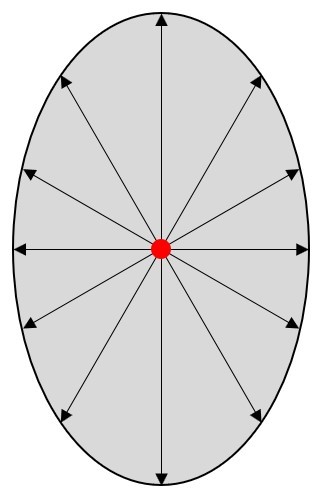
图3.部分偏振光。

任意标量偏振光都可以由两个振动方向相互垂直、相位互相关联的线偏振光的线性叠加来表示；而自然光也可以用两个光矢量振动方向相互垂直、大小相等、相位无关联的线偏振光来表示，但是这两个相位没有关联的光矢量不能合成为一个稳定的偏振光。

接下来，就来详细讲讲偏振光合成。

图4.偏振椭圆。

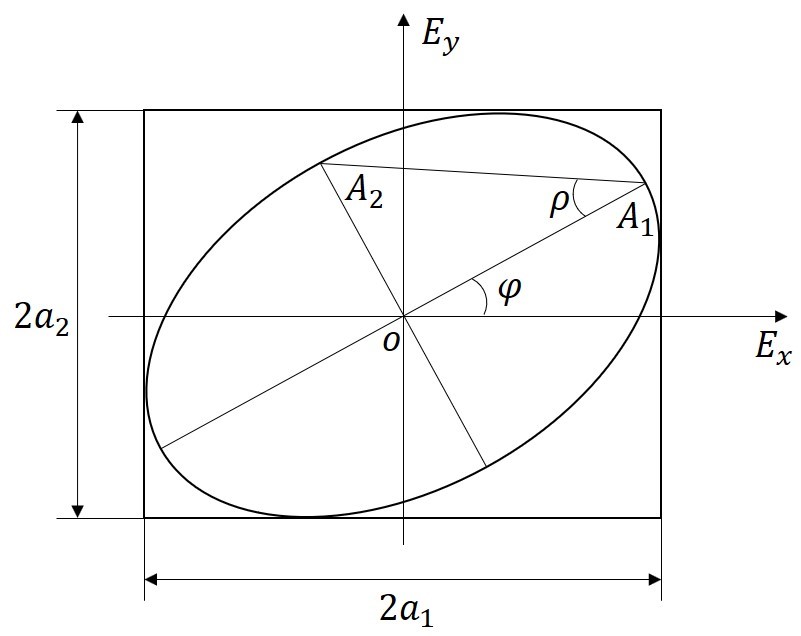
设分别沿\( x \) 方向振动和\( y \) 方向振动的两个\( \varepsilon<0 \) 正交单色光波，传播方向均沿\( z \) 轴，其光场表达式可以写为：

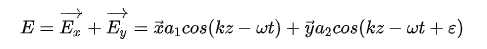
式中，\( \varepsilon \) 代表两个单色光波的相位差，\( \varepsilon>0 \) 说明\( \overrightarrow{E_{y}} \) 要达到与\( \overrightarrow{E_{x}} \) 相同的振幅值，在时间上要滞后\( \varepsilon/\omega \) ，\( \varepsilon<0 \) 意味着\( \overrightarrow{E_{y}} \) 领先\( \overrightarrow{E_{x}} \) 。两个光波合成之后的光振动为这两个正交单色光的矢量和：

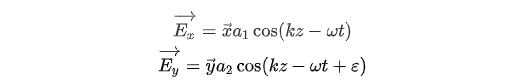
消去时间参数\( t \) ，可以得到合振动光矢量端点的运动轨迹为：

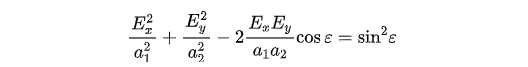
一般情况下，上式代表的是一个椭圆方程，且该椭圆内接于边长分别为\( {2a}_1 \) 和\( {2a}_2 \) 的长方形，如图4所示。

下面我们根据两个正交光波的振幅比和相位差来具体分析合成光的偏振态。

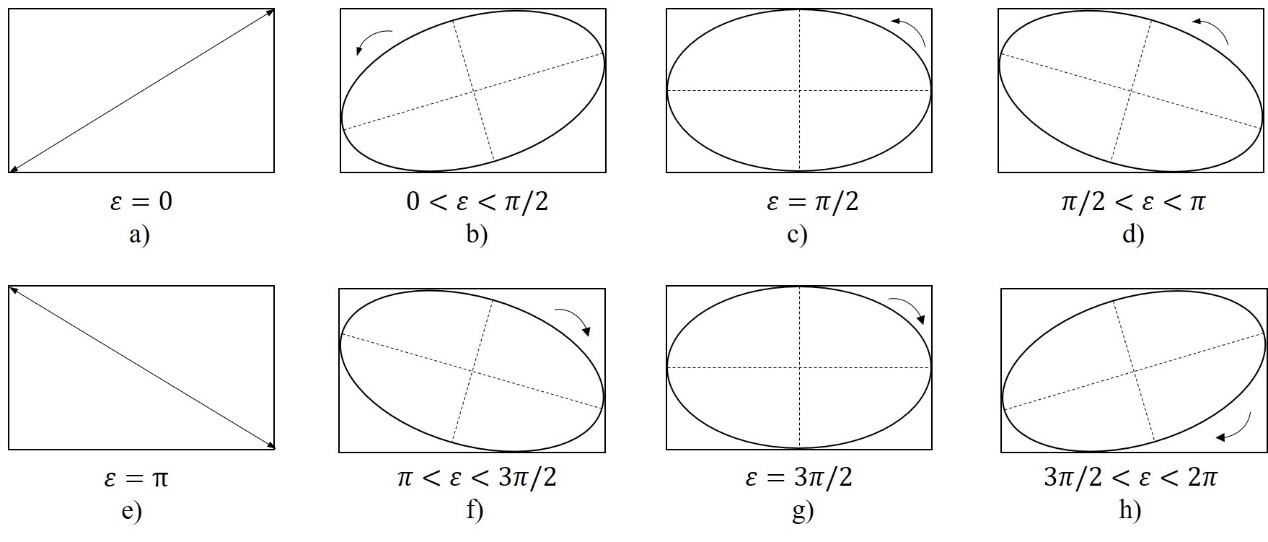
图5.不同相位差对应的偏振态。

1）相位差\( \varepsilon=0 \) 或\( \pm 2\pi \) 的整数倍时，有：

\[ E_y=\frac{a_2}{a_1}E_x \]

此时合成光矢量端点的轨迹为一条经过坐标原点，斜率为\( a_2/a_1 \) 的直线，表明合成光是线偏振光，如图5a。

2）相位差\( \varepsilon=\pm \pi \) 的奇数倍时，有：

\[ E_y=-\frac{a_2}{a_1}E_x \]

此时合成光矢量端点的轨迹为一条经过坐标原点，斜率为\( -a_2/a_1 \) 的直线，合成光也是线偏振光, 如图5e。

3）相位差\( \varepsilon=\pm \pi/2 \) 的奇数倍时，有：

\[ \frac{E_x^2}{a_1^2}+\frac{E_y^2}{a_2^2}=1 \]

此时合成光矢量端点的轨迹为一个正椭圆方程，椭圆的圆心在坐标原点，长轴、短轴分别在\( x \) ，\( y \) 坐标轴上，表明合成光是一个椭圆偏振光, 如图5c、5g。若更进一步，有\( a_2=a_1=a \) ，则上式化为：

\[ E_x^2+E_y^2=a^2 \]

这时合矢量端点的轨迹是一个正圆，因此合成光是一个圆偏振光。

4）相位差\( \varepsilon \) 取其他值时，椭圆方程表征的是任意方位角的椭圆偏振光，如图 5b、5d、5f、5h所示，其长轴方位角\( \varphi \) 由下式决定：

\[ \tan2\varphi=\frac{2a_1a_2}{a_1^2-a_2^2}\cos\varepsilon \]

◆ ◆ ◆

椭圆偏振光可以分别由两组参量来表示，第一组参量是合成光矢量在\( x \) 、\( y \) 轴上的偏振分量\( E_x \) 、\( E_y \) 的振幅比\( a_2/a_1 \) 和相位差\( \varepsilon \) ，第二组参量是椭圆长短轴的长度\( A_1 \) 、\( A_2 \) 及长轴相对于\( x \) 轴的方位角和旋转方向，这两组参量可以通过几何关系相互换算。

将合成光矢量在\( x \) 、\( y \) 轴上的偏振分量\( E_x \) 、\( E_y \) 分别投影到椭圆的长轴、短轴上，再经过几何换算，可以得到椭圆的长轴、短轴长度\( A_1 \) 、\( A_2 \) 与\( E_x \) 、\( E_y \) 的振幅比\( a_1 \) 、\( a_2 \) 有如下关系：

\[ A_1^2+A_2^2=a_1^2+a_2^2 \]

即不管将椭圆偏振光投影到什么坐标下，两个相互垂直的偏振分量振幅的平方和是一个常数。椭圆长轴的方位角可通过4）中的公式计算。如图2.1，进一步定义椭圆度\( \rho \) ，有：

\[ \tan\rho=A_2/A_{1},\left|\rho\right|\le\pi/4 \]

\( \rho<0 \) 时代表右旋圆偏振光，\( \rho>0 \) 时代表左旋圆偏振光。定义振幅比角参数\( \beta \) ：

\[ \tan\beta=a_2/a_{1},0\le\beta\le\pi/2 \]

则有以下关系式：

\[ \sin2\rho=\sin2\beta \sin\varepsilon \] \[ \tan2\varphi=\tan2\beta\cos\varepsilon \]

根据以上两组椭圆偏振参量之间的关系式，即可通过一组参量求取另一组参量。实际工作中可以通过直接测量椭圆偏振光的两个基本参量\( A_2/A_1 \) 和方位角\( \varphi \) ，然后利用它们与\( a_1 \) 、\( a_2 \) 和相位差\( \varepsilon \) 之间的关系，进行偏振光的测定。

下一堂课，我们来讲讲偏振光的产生方法，敬请期待~

{{item.product_sn}}

{{item.category_name}}