LBTEK光学研发团队致力于为广大科研、工业客户提供优质的产品和服务。 团队成员全部是硕士以上学历,其中20%以上具有博士学历,团队成员来自国内外知名企业及高校,深耕科研和工业行业多年,具备扎实的光学理论基础,及仿真算法、生产工艺、实验系统设计和集成器件开发经验。
补偿器其实质是一种在一定范围内延迟量可调的可变波片,它能够产生连续改变的相位差。 按照补偿器结构的不同,可以分为 巴比涅( Babine)补偿器和索累(Soleil)补偿器。
巴比涅补偿器
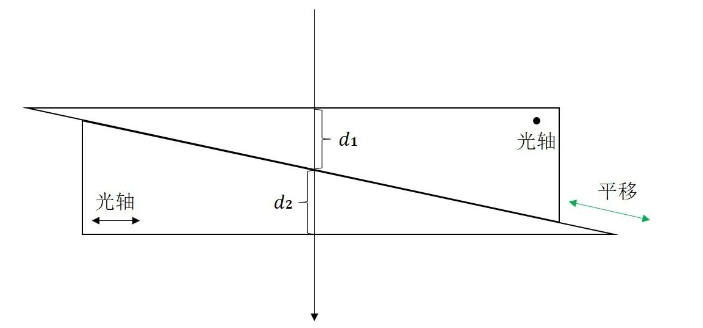
巴比涅补偿器通过晶片平移的方法来改变其相位延迟量,其构造非常简单,图 1是巴比涅补偿器的典型结构,它由两块双折射晶体制成的光楔相对组合而成,两块光楔的光轴互相垂直。 光束垂直正入射时,分解成光矢量相互正交的两个偏振分量,且在上面光楔中的o光、e光,在下面光楔中将相应变成e光、o光。 假设材料为正晶体,光束通过补偿器后两个偏振分量之间的相位差为:
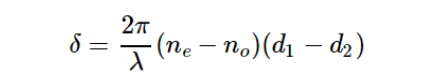
索累补偿器
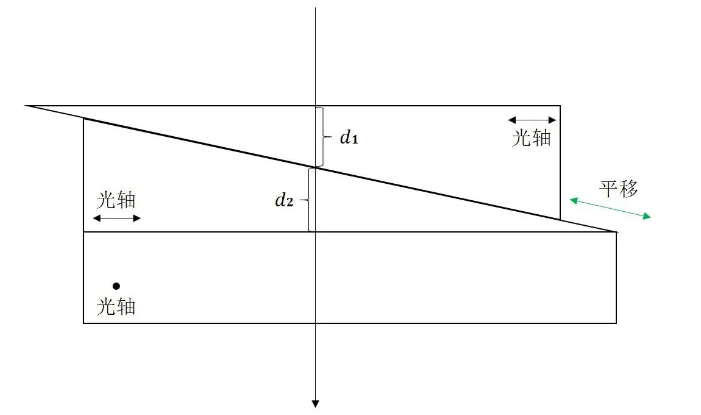
图2.索累补偿器。
索累补偿器的结构与巴比涅补偿器略有不同,它由两个双折射光楔和一个平面晶片组合而成。 其中一个光楔可以 平移,另一个光楔固定在平面晶片上。 如图2所示,两个双折射光楔的光轴方向一致,平面晶片的光轴与光楔光轴垂直。 平移上面的光楔,可以使光楔楔厚发生变化,继而改变光楔所产生的相位延迟量。 光楔延迟量与平面晶片延迟量的差值就是索累补偿器总的相位延迟量,通过平移光楔,实现了补偿器延迟量的连续可调。 并且索累补偿器两个光楔接触区域内的相位延迟量完全一致,这一点注意与巴比涅补偿器区别。
由于补偿器能在很大的波长范围内实现所需的相位延迟量,可以补偿或者抵消一个偏振器件的双折射,因此广泛应用于波片相位延迟量的测量。 实际使用中,索累补偿器通常通过精密数显千分尺或者伺服电机来驱动光楔平移,以便校准和读取补偿器的延迟量。
严格来讲,补偿器可以定义为一种可变波片。 除了巴比涅补偿器和索累补偿器之外,电控液晶波片也是一种可变波片。 在液晶盒上施加可调电压,驱动液晶分子进行偏转,液晶分子的指向矢发生变化,从而改变相位延迟量,具体不再赘述。
前面介绍了用于将非偏振光变成偏振光的起偏器件,接下来将介绍另一种相反的偏振光学元件,即将偏振光变成非偏振光的退偏器。 大部分的光探测器都对光的偏振态比较敏感,如果不对入射光进行退偏处理,将极大地影响探测精度。 因此退偏器在光纤通信、天文观测、激光加工、光纤陀螺等场景中具有广泛的应用。
和起偏器件一样,退偏器也大多采用双折射材料制作而成。 根据退偏器所针对的偏振光不同,可以分为复色光(包括白光)退偏器、单色光退偏器和单色光圆退偏器,下面将分别进行介绍。
复色光退偏器
最普通的复色光退偏器其实就是一块普通的波片,它由单片平行平板双折射晶体构成,其光轴与通光面平行。 线偏振复色光垂直正入射,其振动面与平板晶体光轴成45°角。 不同波长的入射偏振光通过平板晶体后具有不同的相位延迟,变成不同椭圆度的椭圆偏振光出射,因此从平行平板晶体同一位置出射的光将具有不同的偏振态,整个光束就是各种随机偏振光的集合体,从而在光束横截面上实现了消偏的积分效果。

单片式复色光退偏器要求入射偏振光振动面与光轴成45°的时候才具有较好的退偏效果,为了对不同偏振方向复色偏振光实现有效退偏,应采用Lyot退偏器。 图3是 Lyot 退偏器的结构示意图,它由两块楔形双折射晶体组成,两块晶体的厚度不同,厚楔形晶体与薄楔形晶体的厚度比为2:1,光轴夹角为45°。 线偏振单色光入射时,通过Lyot退偏器后,不同位置出射光的 o 、e偏振分量的相位差不同,具有不同的偏振态,从而改变其有序状态,使出射光的偏振度下降; 线偏振宽光谱复色光入射时,不同波长的光通过Lyot退偏器后变为具有不同椭圆度的椭偏光,整个光束就是各种随机状态的合成,使输出光呈现消偏,即在频域上产生了消偏的积分效果。 Lyot退偏器的消偏效果与工作波长、材质、光轴夹角和棱镜楔角有关。 经退偏器出射的光和自然光的区别是: 前者在不同位置的偏振态是确定的,而后者不同位置的偏振态是随机的。 一般来说,只要使光在不同的偏振方向上不占优势,就认为达到了消偏效果。 可以知道,Lyot退偏器对单色、复色光以及不同偏振方向的线偏振光和部分偏振光都具有良好的退偏效果。
单色光退偏器
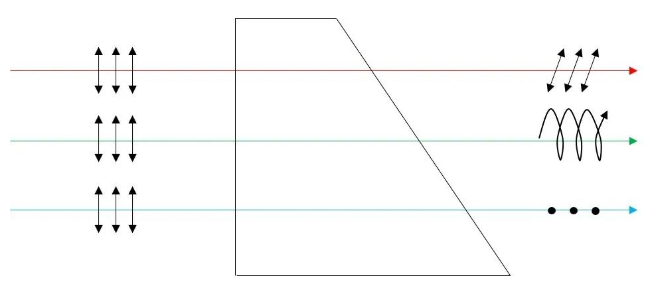
双折射 单光楔单色光退偏器 结构如图4所示,其工作原理与平行平板复色光退偏器类似,其不同之处在于: 平行平板复色光退偏器针对复色光入射,波长的不同即造成了经过相同厚度的双折射材料,不同波长光的 o 、e偏振分量的相位差不同; 而单光楔单色光退偏器针对单色光入射,需要通过不同厚度的双折射材料,出射面不同位置处的o、e偏振分量才会具有不同的相位差,因此要制成楔形。
单色圆退偏器
单色圆偏光退偏器用于对圆偏振光退偏。 圆偏光退偏器就是将一个1/4波片与两块双折射光楔胶合而成,其中两块双折射光楔的光轴相互正交,组成一个线偏振退偏器。 入射圆偏振光先经过1/4波片变成线偏振光,再经过线偏振退偏器实现退偏。 为达到最佳退偏效果,线偏振光的偏振方向应与第一片双折射光楔的光轴成45°角。 单色圆偏光退偏器对左旋圆偏光和右旋圆偏光均有很好的退偏效果。
除了上述退偏器之外,还有其他结构和材质的退偏器,原理更为复杂,详情请参考相关资料。
法国物理学家阿拉果首先发现线偏振光沿着石英晶体的光轴传播时,线偏振光的光矢量将随着传播距离而逐渐转动,这种现象称之为旋光性,具备旋光性的介质称为旋光物质:
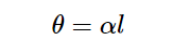
其中,θ为光矢量转过的角度,l为线偏振光在物质中通过的距离,α为旋光系数,代表光传播1 mm的距离后,光矢量转过的角度。 自然界中许多物质都具有旋光性,例如石英晶体、酒石酸、松节油、砂糖。 和圆偏振光一样,旋光性也有左旋和右旋之分,逆着光传播方向观察,光矢量方向顺时针旋转为右旋,逆时针旋转为左旋。
需要指出的是,旋光晶片使得入射线偏振光光矢量发生偏转的作用虽然与半波片的作用有些类似,但两者是有本质区别的: 半波片光轴平行与晶面,旋光晶片光轴垂直于晶面; 半波片只针对特定波长,旋光晶片可应用于任何波长,只是不同波长转动角度不同; 半波片可以使入射线偏振光光矢量左转,也可以右转,左转或右转以及转动角度的大小与线偏振光光矢量方向相对于波片快慢轴的夹角有关,而确定旋向和厚度的旋光晶片只能使线偏振光的光矢量朝着一个方向转动一定角度。
除了某些物质固有的旋光性之外,法拉第发现,另外有一些本来不具备旋光性的物质在外界磁场作用下产生了旋光性,这就是磁致旋光效应,又叫做法拉第效应,如图5。 其中,入射光矢量转过的角度θ大小与施加在非磁性物质上的磁感应强度B及光在物质中经过的距离l成正比,其中V是维尔德物质常数,与波长相关。
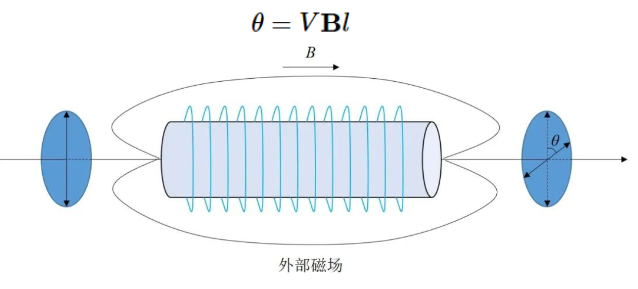
图5.法拉第效应。
利用法拉第效应可以制成旋光器,它由强力永磁体绕铁磁晶体构成。 线性偏振光经过法拉第旋光器后,其光矢量振动方向会旋转45°,而不受输入偏振方向的影响。 法拉第旋光器是一种非互易光学元件,从旋光器对侧进入的线偏振光会继续相对于旋光器在相同的方向上旋转。
LBTEK提供的自由空间隔离器就是利用了法拉第旋光器的非互易性,它由输入偏振光学元件、法拉第旋光器以及输出偏振光学元件三部分构成,如图6。 其中输入与输出偏振光学元件的偏振透过方向夹角为45°。
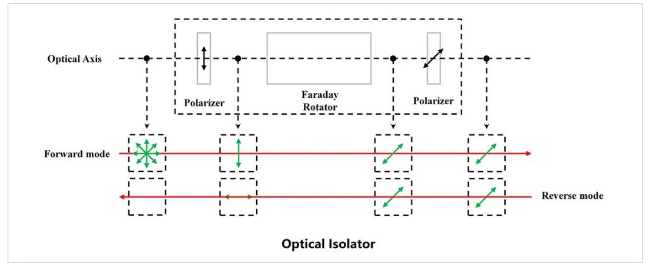
图6.自由空间光隔离器。
可见,磁致旋光效应在激光放大装置、光纤通信装置中有广泛的应用。 除此之外,磁致旋光效应还可用于磁光调制、自动检测等领域。
通过前面的内容,我们了解了用于产生偏振光或者对偏振光进行变换的光学器件,本节将介绍一种用于检测偏振光状态的偏振器件: 偏振测量仪。 测量偏振光的方法有很多,本节介绍的偏振测量仪采用的是旋转1/4波片法。
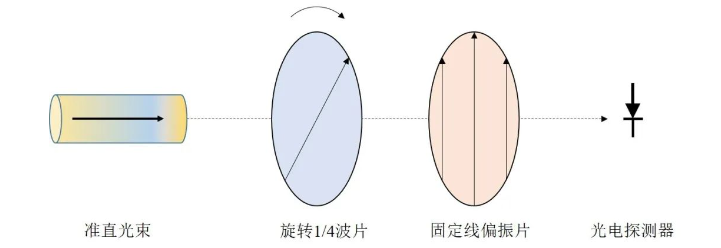
图7.偏振测量仪光路图。
图7是偏振测量仪的光路原理图,准直平行单色激光入射到真零级1/4波片上,再经过一个固定的线偏振片,被光电探测器接收。 1/4波片可以旋转,改变入射光的偏振态,从而调制通过固定线偏振片入射到光电探测器上的光振幅。 准直光束、旋转1/4波片、固定线偏振片的偏振特性都可以用穆勒矩阵来表示,通过穆勒矩阵计算,得到 光电探测器接收到的光强表达式 。 光电探测器将接收到的调制光强转化为光电流,光电流包含直流项和相移项,其系数与波片旋转频率成一定比例关系,通过傅里叶分析法可以得到直流项和相移项的系数,再结合光电探测器接收到的光强表达式反算出入射光束的斯托克斯参量,从而得到入射光的偏振态。