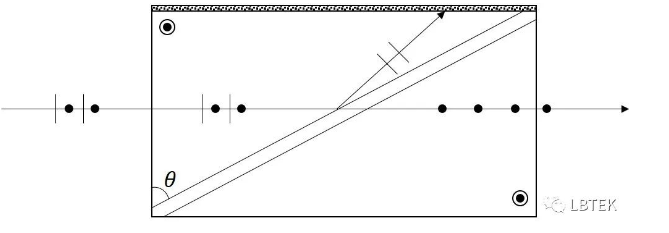
格兰-傅科棱镜 也是由两块直角方解石棱镜组成，与 格兰 -汤普森棱镜不同的是，两块方解石棱镜中间不是胶合剂，而是空气隙。 格兰-傅科棱镜 的缺点在于AOI（Angle of incidence，入射角）范围较小，约为10°左右，而格兰-汤普森棱镜的AOI范围可以达到30°左右。 但是格兰-傅科棱镜的光损伤阈值要远远大于格兰-汤普森棱镜，可以承受上限高达100w/cm²的光功率密度，这是因为空气介质的稳定性要远超胶合剂。

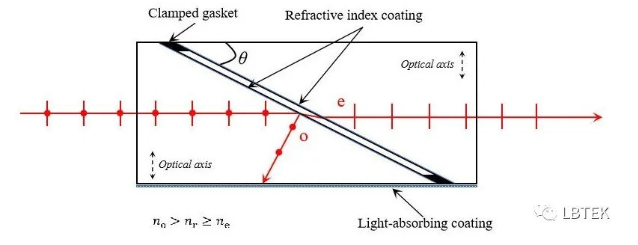
图2.格兰-泰勒棱镜。

格兰系列的偏振棱镜还有格兰-泰勒棱镜。 格兰-泰勒偏振棱镜由两块光轴相互平行的负单轴晶体棱镜配合而成。 如图2所示，平行自然光自棱镜左边端面垂直入射时，入射光的两个正交分量均不发生偏折，但各自的速率与折射率不同。 其中，振动方向垂直于棱镜光轴的分量（即s分量）为o光，相应的折射率为n_o，振动方向平行于光轴的分量（即p分量）为e光，相应的折射率为n_e。 因为棱镜材料为负单轴晶体，有n_o > n_e，因此，o光比e光更容易发生全反射。 两棱镜交界面处斜面上均镀有折射率为n_r的涂层，n_r大于并非常接近于n_e但小于n_o，所设计的棱镜楔角θ大于o光在斜面上的全反射临界角θ₀（=arcsin(n_r/n_o)），入射光传输至交界处斜面时，o光发生全反射，同部分被反射的e光一起向下传输，被下方的涂层吸收，而e光平行出射。 白光入射时，透射端可得到无色散的线偏振光。

格兰-激光棱镜 的工作原理和格兰-泰勒没有太大的不同，区别在于o光发生全反射后，在下方分界面处折射出射，而不是被吸收。

偏振分束棱镜 与偏振起偏棱镜的区别是让入射光分解的正交线偏振o光和e光都可以通过，从而获得两束分开的线偏振光，常用于偏振光干涉系统或用作起偏器。

图3所示的沃拉斯顿棱镜是一种典型的偏振分束棱镜，它由两块底部相同、光轴正交的双折射晶体（可以是石英、方解石、α-BBO…，本例以方解石为例）棱镜胶合而成。 平行自然光正入射到棱镜端面，在第一块棱镜内o光、e光以相同的方向、不同的速度相前传播； 在第二块棱镜内，由于其光轴与第一块棱镜正交，o光变成了e光，方解石n_o>n_e，相当于由光密介质到光疏介质传播， 因此远离棱镜斜面法线传播 ； e光变成了o光，相当于由光疏介质到光密介质传播，因此靠近棱镜斜面法线传播。 o光、e光在从第二块棱镜直角面出射时，属于光密到光疏介质传播，向着远离直角面法线的方向偏离，从而得到角度分开，振动方向垂直的两束线偏振光。 沃拉斯顿棱镜允许入射光从左、右任何一个直角面入射，效果不变。 但如果入射光是非单色光，出射的两束线偏振光会有轻微的色散现象。

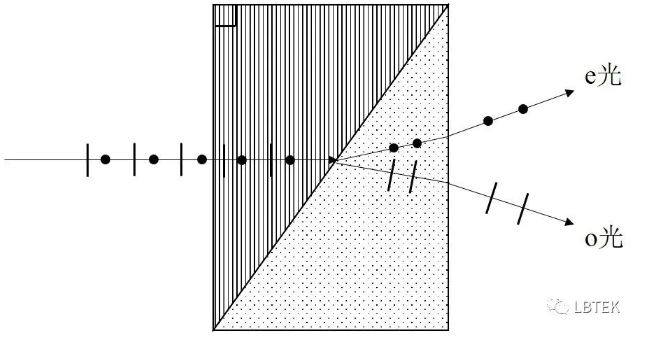
洛匈棱镜 的结构与沃拉斯顿棱镜基本相似，区别在于： 沃拉斯顿棱镜中， 两块直角棱镜的光轴不但互相正交 ，且都与光的入射方向正交； 而洛匈棱镜中，两块直角棱镜的光轴互相正交，但是第一块棱镜的光轴与入射方向平行，只有第二块棱镜的光轴与入射方向垂直。 如图4，是洛匈棱镜一种典型结构，由两块底部相同、光轴正交的双折射（本例以石英晶体为例）晶体构成。 平行自然光正入射到棱镜端面，在第一块棱镜内沿光轴传播，不发生双折射，垂直于纸面振动的分量和平行于纸面振动的分量都是o光，以o光光速向前传播； 在第二块棱镜内，其光轴与第一块棱镜正交，垂直于纸面振动的分量变成了e光，由于石英n_e>n_o，相当于由光疏介质到光密介质，因此靠近棱镜斜面法线传播； 平行于纸面振动的分量依然是o光，折射率不变，沿原入射方向无偏折地从棱镜出射。 最后得到角度分开，振动方向垂直的两束线偏振光。 洛匈棱镜只允许入射光从左直角面入射，并且使o光无偏折地出射。

偏振分束镜的作用也是将入射的非偏振光分成两束线偏振的s光和p光，与偏振棱镜不同，偏振分束镜使得s光反射、p光透射。 按照基本结构和原理的不同，偏振分束棱镜可以分为偏振分束立方体和平板偏振分束镜。

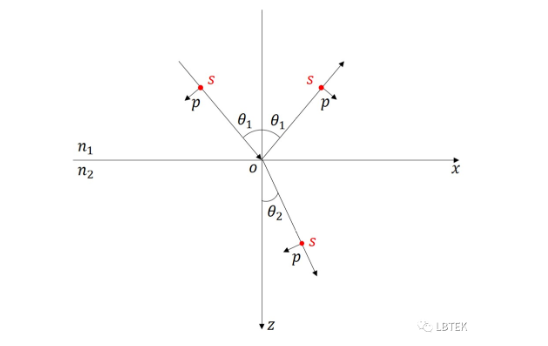
图5.光在电介质界面上的反射和折射。

光入射到两个不同的电介质界面上会发生折反射现象。 我们知道，任意方向振动的光矢量都可以分解为互相正交的两个分量，如图5，将入射光分解成垂直于入射面振动的s波和平行于入射面振动的p波，显然s波和p波都是线偏振光。 我们分别考虑s波和p波的折反射现象。

根据菲涅尔公式，可以得到s波、p波的振幅反射系数和振幅透射系数公式：

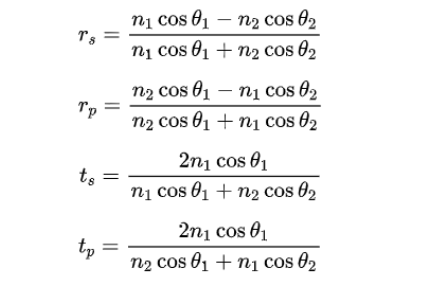
由上面的式子可知，如果入射角θ₁和折射角θ₂满足θ₁+θ₂=π/2，那么有n₂cosθ₁=n₁cosθ₂，此时反射光中没有p波成分，只有垂直于入射面振动的s波，发生全偏振现象，这时反射光是光矢量垂直于入射面振动的线偏振s光，透射光是偏振度很高的部分偏振光（p光占优势），此时θ₁称为布儒斯特角，也记作θ_B。 根据这一特性，我们可以采用大折射率介质来提高反射光的反射比，以此获得反射线偏振光（s光）； 也可以通过多层介质堆叠来逐步去除透射光中的s光成分，提高透射光的偏振度，获得线偏振的透射光（p光）。

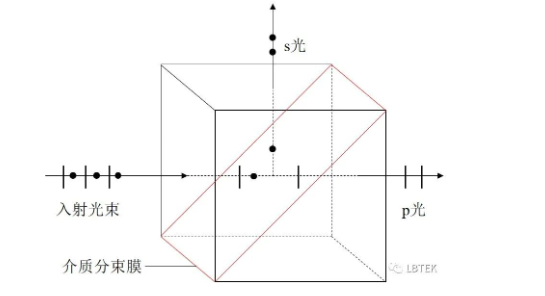
如图6， 胶合棱镜型偏振分束镜 就是根据折反射原理制成，在两块等腰直角玻璃棱镜之间交替镀上高折射率和低折射率膜层，胶合成立方体棱镜。 入射光垂直于棱镜表面，以 45 度角入射到多层介质膜上，经过膜层的反射和透射，反射的s偏振光与透射的p偏振光垂直于棱镜表面，成90度夹角分开出射。

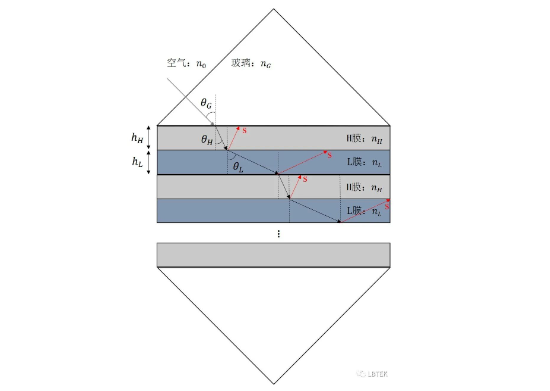
如图7，是棱镜型偏振分束镜中多层偏振介质分光膜的工作原理示意图。 入射光经过玻璃介质（折射率为n_G），以角度θ_G入射到多层介质膜上。 介质膜由高折射率膜层（折射率为n_H）和低折射率膜层（折射率为n_L）交替组合而成，n_L<n_G<n_H。 由折射定律，有：

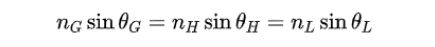
为使每个高、低折射率介质膜界面上的反射光中没有p光成分，θ_H和θ_L需满足布儒斯特条件θ_H+θ_L=π/2，即两种介质膜的p光有效折射率必须相等：

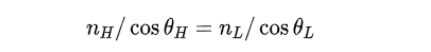
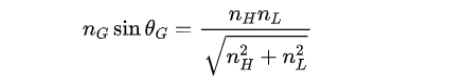
另外除了满足上式表示的布儒斯特全偏振反射条件，确保膜层界面上反射的只有线偏振的s光之外，膜层的厚度选择也有要求。 根据菲涅尔公式可知，不管入射角θ₁取何值，s光、p光的振幅透射系数t_s、t_p始终为正值，这说明折射光的相位与入射光相位相同，不发生相位突变。 对于 s 光、p光的振幅反射系数r_s、r_p，可分情况讨论：

• 当光从光疏介质到光密介质（L膜→H膜），r_s始终为负，说明反射的s 光有π的相位变化；
• 当光从光疏介质到光密介质（L膜→H膜），如果 θ_H+θ_L <π/2，即入射角小于布儒斯特角θ_B时，r_p为正，p光相位变化为零； 如果θ_H+θ_L>π/2，即入射角大于布儒斯特角θ_B时，r_p为负，p光相位变化为π；
• 当光从光密介质到光疏介质（H膜→L膜），如果入射角大于全反射临 界角θ_C（θ_C>θ_B）时，s光、p光都发生相位突变，且相位变化由0缓慢增加到π；
• 当光从光密介质到光疏介质（H膜→L膜），如果入射角小于全反射临 界角，s光、p光的相位变化情况刚好与L膜→H膜的时候相反，且入射角等于布儒斯特角的时候发生全偏振现象。

膜层厚度的选择应当遵循膜层上下表面反射s光干涉加强的原则，根据s光、p光的振幅反射系数r_s、r_p变化情况，当入射角满足布儒斯特角全偏振条件时，在H膜→L膜界面处，s反射光没有相位变化； 在L膜→H膜界面处，s反射光有 π 的相位变化，即膜层上下表面s反射光始终存在因相位突变产生的大小为π的相位差，因此膜层厚度应当满足 λ/4 膜系的条件，膜层上下表面s反射光由光程差引起的相位差δ为π，总的相位差为2π，产生干涉加强，即：

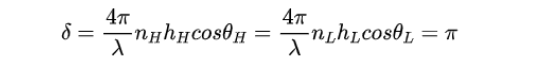
综上，通过合理选择玻璃材料的折射率和膜层材料、厚度及层数等参数，可以实现光束的最大偏振度和消光比。 增大高、低折射率膜层的折射率差，可提高反射率； 棱镜材料折射率的选取，应该确保光从棱镜中入射到多层介质膜上时，折射角（也就是高、低折射率薄膜界面上的入射角）等于布儒斯特角，使反射光为线偏振的s光； 膜层层数则取决于对反射光和透射光偏振度的要求； 膜层厚度应该满足膜层上下表面干涉加强的条件。

需要指出的是 ，偏振分束立方仅仅在特定的入射角下才能实现全偏振 ，但是实际应用中入射角会存在一定的波动性，或者是一束未完全准直的发散/会聚光，因此必须了解偏振分束立方在入射角波动情况下的特性。 当膜层界面处的入射角偏离了布儒斯特角，反射光中依然有s光成分，且其振幅反射系数没有太大变化，但是反射光中还产生了p光成分，因此反射光的消光比会迅速下降，而透射光依然保持较高的偏振度。 但由于一部分P光发生了反射，因此透射光的光强会随之降低。 可见偏振分束立方的偏振分束特性对于入射角十分敏感。

上述偏振分束立方是基于布儒斯特角入射，因此偏振分束介质膜要胶合在高折射率的棱镜中间，光从棱镜介质中入射到分束膜层上，才能满足布儒斯特角全偏振条件。 除偏振分束立方外，还存在一种从空气入射到分束介质膜上的平板分束镜。 平板分束镜也是基于折反射原理，但并不是通过布儒斯特角来产生偏振效应。

如图8所示，是偏振平板分束镜的工作示意图。 在熔融石英玻璃基底上镀窄带偏振分束膜系。 入射光从空气介质中以45度角入射到分束膜上，分成透射的p偏振光和反射的s偏振光。 需要指出的是，平板偏振分束镜p光的高透射率是通过干涉效应实现的（偏振分束立方p光不干涉，其高透射率是通过布儒斯特角全偏振效应来实现的），其作用机理类似于长波通干涉滤光片，基本膜系结构为：

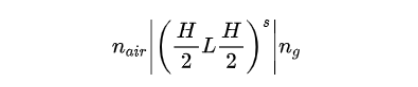
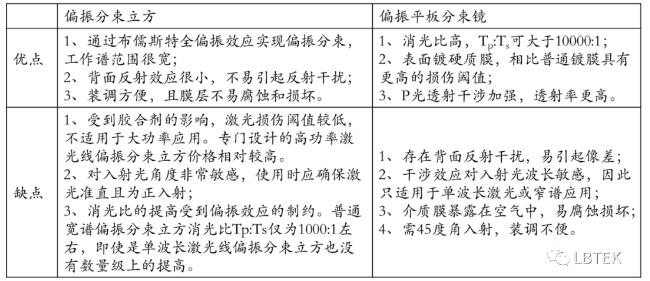
胶合棱镜型 偏振分束立方 和平板偏振分束镜都可以将非偏振光分成偏振的s光和p光，两者各有优缺点，对比如下：