LBTEK光学研发团队致力于为广大科研、工业客户提供优质的产品和服务。 团队成员全部是硕士以上学历,其中20%以上具有博士学历,团队成员来自国内外知名企业及高校,深耕科研和工业行业多年,具备扎实的光学理论基础,及仿真算法、生产工艺、实验系统设计和集成器件开发经验。
在光学领域经常要用到这样一类光学器件,用来 产生、改变或检测 光的偏振特性,又或者 利用 光的偏振特性来进行一些物理参量的测试、信息的记录与传递、特定光学现象的实现等,这就是偏振光学元件。 典型的偏振光学元件包括偏振片、波片、涡旋波片、偏振棱镜、偏振分束镜、补偿器、退偏器、旋光器、偏振测量仪,接下来将系统地介绍这些偏振器件。
偏振片是最基础的偏振光学元件,它的作用是将自然光或部分偏振光变成线偏振光。 将偏振片细分,可以分为金属线栅偏振片、纳米粒子偏振片、 二向色薄膜偏振片 等类型,这些偏振片各具有不同的特性和优点。
金属线栅偏振片
图1为金属线栅偏振片示意图,线栅的间距小于入射光波长。 非偏振光入射到金属线栅上,平行于 线栅排列方向的偏振光分量 Ep被金属线栅反射,或因为对金属线栅的内部电子做功而被吸收,垂直于线栅排列方向的偏振光分量Es透过线栅继续传播,从而得到线偏振光。
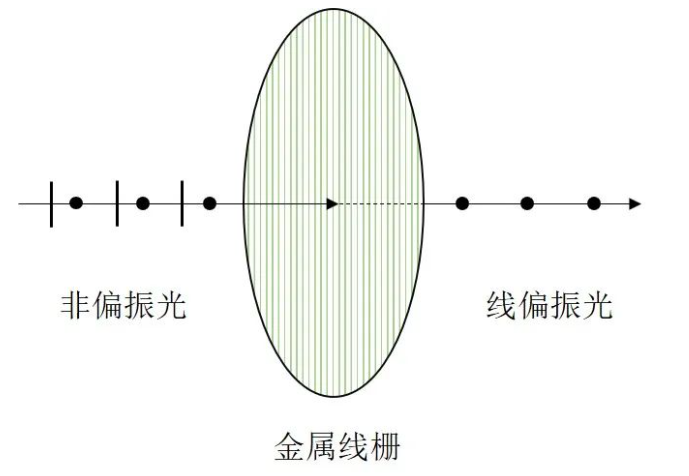
普通金属线栅偏振片是在两片保护玻璃基底之间夹持金属线阵列制作而成,除此之外,还有一种全息金属线栅偏振片,它是通过全息方法在基底(一般是BaF2、CaF2、KRS-5或ZnSe红外透明材料)上制备线性凹槽,然后将金属沉积在这些凹槽上形成线栅。 传统金属线栅偏振片 适用于深紫外波段到中红外波段的光源 ,消光比较高(除了紫外波段),而全息金属线栅偏振片适用于中红外波段到远红外波段的光源,消光比较低,用户可根据自身需要进行选择。
纳米粒子偏振片
纳米粒子偏振片 是在硅酸钠玻璃薄膜中嵌入长椭球形纳米粒子,再夹持在两片保护玻璃之间制备而成,它产生偏振光的机理类似于传统的二向色性双折射聚合物偏振片,吸收 偏振方向垂直于透射轴的光分量 ,透过偏振方向平行于透射轴的光分量。 与传统聚合物偏振片不同的是,纳米粒子偏振片具有更高的激光损伤阈值和消光比,适合对偏振度有较高要求的高能激光应用。
二向色薄膜偏振片
除了部分各项异性的双折射材料具有二向色性,某些各向同性介质受到外界作用时也会产生二向色性。 将PVA(聚乙烯醇)薄膜浸泡在碘溶液中,形成碘-聚乙烯醇分子碘链,然后在高温下拉伸,使碘链沿着拉伸方向规则排列,形成具备导电功能的长碘链,碘中的传导电子就可以沿着碘链的方向运动。 当自然光入射时,平行于碘链方向的电场分量会驱动碘链中的传导电子运动,从而因为对电子作功被吸收; 垂直于碘链方向的电场分量因为不对电子做功而透过,最终使得透射光为垂直于碘链方向偏振的线偏光。 通过这种方法制备的偏光片可以在整个可见光谱范围内实现98%以上的偏振度,且由于工艺成熟,价格低廉,可以很方便地制成大面积的偏光膜,因此在显示器件上得到了广泛的应用。

图2是显示屏的结构示意图,偏光膜(POL)在其中扮演着关键的角色。 从背光源发出的光为380 nm~780 nm的非偏振白光,经过下POL后变成线偏振光。 LC(液晶层)填充具有双折射特性的液晶分子,TFT阵列基板在外部输入电信号的作用下,能够驱动每个亚像素内的液晶分子旋转,从而改变经过每个亚像素的线偏振光的偏振方向。 从下POL出来的线偏振光经过液晶层后,每个亚像素对应的线偏振光都具有各自独立的偏振方向,再经过CF(彩色滤光片)后,分别变成红、绿、蓝三原色线偏振光。 在CF上方还有上POL,三原色线偏振光经过上POL,由于各自偏振方向不同,因此透过上POL的光强不同,每个像素中不同强度的红绿蓝三原色合成为各种颜色的色光,从而形成整个屏幕的彩色画面。 显然,从显示器屏幕出射的光为线偏振光,其偏振方向与上POL的透过方向一致,拿一个线偏振片放在眼睛前方,转动线偏振片,能够很明显地观察到显示器发出的光发生明暗变化。
以上所述偏振片都是用于产生线性偏振光的线偏振片,还有一类用于产生圆偏振光的圆偏振片。 圆偏振片由线偏振片加1/4波片组成,我们将在下一节波片的内容中具体阐述圆偏振光的产生机理。
波片,又称之为相位延迟片,可使偏振光两个振动方向相互垂直的偏振分量间产生一个相对的相位延迟,从而改变光的偏振特性。 下面我们将从波片相位延迟量的产生机理、波片的分类、波片的作用原理等方面进行介绍。
波片相位延迟量的产生机理

图3.晶体双折射现象。
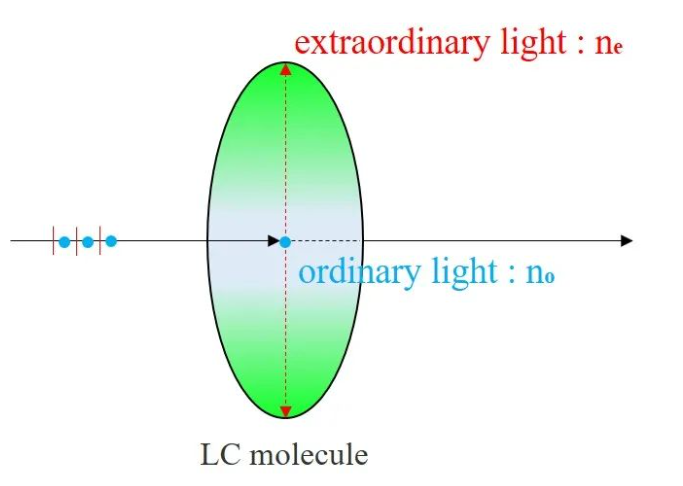
波片大多由双折射材料制造而成。 根据折射定律我们知道,一束单色自然光入射到各向同性介质时,只产生一束折射光。 而当单色自然光在各向异性晶体界面上发生折射时,一般产生两束折射光,这种现象称之为双折射。 两束折射光中,一束为寻常光(o光),一束为非常光(e光)。 其中o光遵循折射定律,折射光线总在入射面内,折射率为no,no为常数。 e光不遵循折射定律,通常情况下,e光折射光线不在入射面内,折射率为ne(θ),θ为入射角度。 用检偏器分别检验o光和e光,可以知道,o光和e光都是线偏振光,如图3所示。
根据晶体双折射现象中o光和e光的折射率差,入射光两个相互正交的线偏振分量之间会产生一个相对的相位延迟。 其中,波速快的光矢量方向为波片的快轴,与之垂直的光矢量方向为慢轴。 对负单轴晶体(ne<no),快轴在e光光矢量方向(即光轴方向,光在晶体中沿此方向传播不发生双折射现象),o光光矢量方向为慢轴; 对正单轴晶体(ne>no),快轴在o光光矢量方向,慢轴在e光光矢量(光轴)方向。 波片的常用材料之一为石英,石英属于正单轴晶体,单色光垂直正入射到石英晶体上,发生双折射,但是o光、e光不分离,只产生相位差:
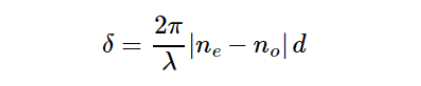
波片正是利用双折射晶体的上述特性来对入射光产生特定的相位差。 根据波片产生的相位差大小,可分为全波片、二分之一波片(又叫半波片)、四分之一波片,分别产生大小为2(m+1)π、2(m+1/2)π、2(m+1/4) π的相位差,其中m为自然数; 当m=0时,称为零级波片,当m≠0时,称为多级波片,其中零级波片又分为普通零级波片和真零级波片。
石英多级波片
石英多级波片 由单片石英晶体制作而成,如图4所示。 入射光经过单片石英晶体,分解成o光和e光。
当 石英晶体厚度d 满足:
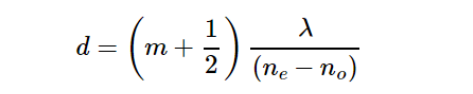
当石英晶体厚度d满足:
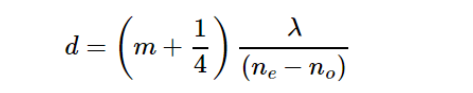
其中,m为大于0的正整数,相位延迟量δ=(2m+1/2)π,即产生m+1/4个波长的相位延迟,此时为石英多级四分之一波片。

图4.单片石英晶体。
石英真零级波片
石英真零级波片也是由单片石英晶体制作而成。
当石英晶体厚度d 满足:
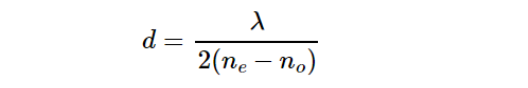
当石英晶体厚度d满足:

普通石英零级波片
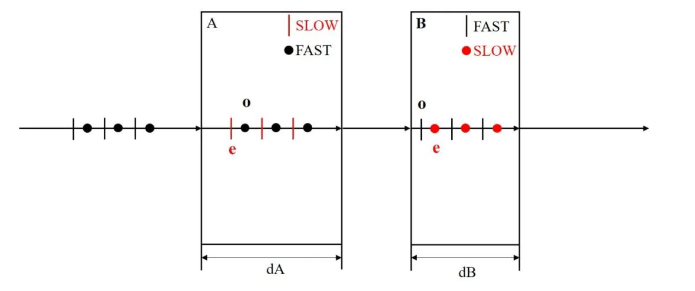
入射光经过第一片多级石英波片,分解成o光和e光,产生相位差 δ1 ; 经过第二片多级石英波片,o光变成e光,e光变成o光,产生相位差δ2。 总的相位延迟量为Δδ:
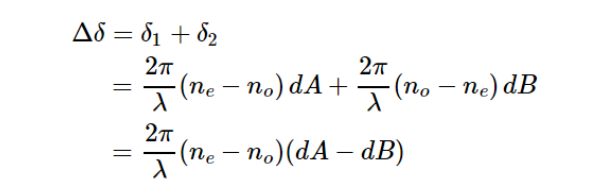
当 dA-dB满足:
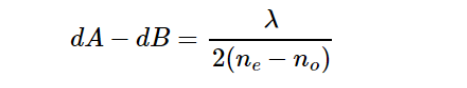
当dA-dB满足:

总相位延迟量∆ δ =π/2,即为石英零级四分之一波片。
液晶聚合物真零级波片
上述波片都是针对单色激光应用设计的,由o光和e光相位差公式可知,当波片的厚度确定时,相位延迟量δ近似随波长线性变化。 我们希望可以消除这种色差效应,当入射为宽谱光源时,波片的延迟量仍然可以维持在一个较小的变化范围内。 设想有一种双折射材料,其双折射率也随波长呈线性变化,那么它的相位延迟量将不再随波长变化而变化。 但实际我们很难找到这种双折射材料,因此需要考虑其他设计来消除色差效应。
消色差波片
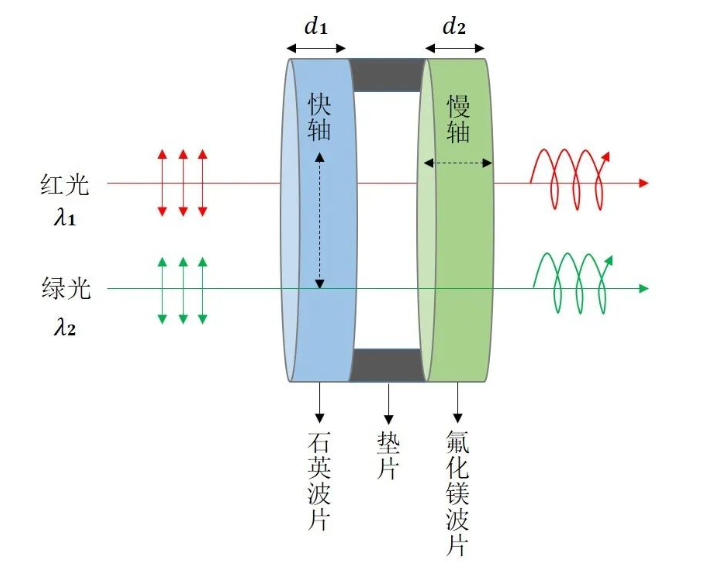
如 图 7所示,一种典型结构的消色差波片是由两个不同的双折射材料快轴与慢轴对准而构成,例如 石英片晶体与双折射氟化镁 或紫外蓝宝石片。 这种结构利用了不同材料双折射率随波长变化不一致的特性, 波长为 λ1的红光和波长为λ2的绿光分别入射到消色差波片上,产生的相位差依次为 δ1 和δ2:
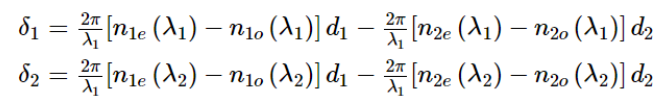
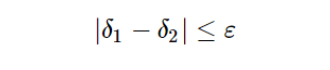
ε为工作带宽内允许的最大延迟量波动。 需要指出的是,消色差波片并不仅限于图7所展示的结构,不同材料的多级组合还可实现更好的消色差效果,例如3片石英片晶体与3片双折射氟化镁组合可以在一个很宽的波长范围内实现更加平坦的“超消色差”效果。 另外,同种双折射材料组合也可以实现消色差,一般是3片同种材料的组合,也可以是3片以上。
菲涅尔菱形棱镜波片
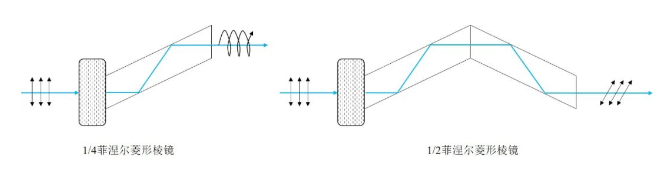
二分之一波片的作用
二分之一波片 也叫做半波片,光正入射时,二分之一波片可以对入射光两个相互正交的偏振分量间产生半个波长,也就是大小为π的相位延迟。 根据二分之一波片的这一特性,可以用来旋转线性偏振光的偏振方向。 下面通过图解方法说明二分之一波片的这一作用原理。
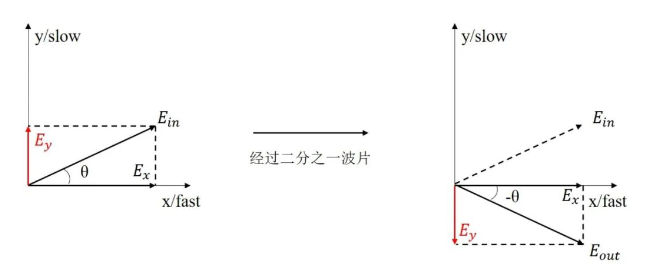
如图9,设波片快轴位于x轴,慢轴位于y轴,线偏振光沿z轴垂直正入射,振幅为A,偏振方向与波片快轴夹角为θ,将入射光分解为沿x轴偏振和沿y轴偏振的两个正交分量:
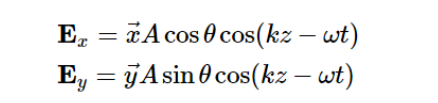
其中,负号代表沿y轴负方向的单位矢量。 可以知道,合成后的光矢量与波片快轴夹角为-θ。 可见,经过二分之一波片后,Ey的振动方向相对Ex转过了180度,因此出射线偏振光的振动方向将向着波片快轴方向转动2θ角度。
四分之一波片的作用
如图10,设波片快轴位于x轴,慢轴位于y轴,线偏振光沿z轴垂直正入射,振幅为A,偏振方向与波片快轴夹角为θ,将入射光分解为沿x轴偏振和沿y轴偏振的两个正交分量:
其中,负号代表沿y轴负方向的单位矢量。 根据叠加原理,合成后的光矢量为:
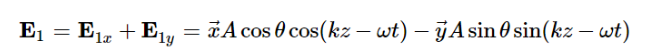
消去时间相位因子,可以得到合成光矢量末端的运动轨迹满足:

可见,线偏振光经过四分之一波片后,出射光将变为椭圆偏振光。 椭圆偏振光的 长轴为 Acosθ,短轴为Asinθ。 特别地,当入射光偏振方向与四分之一波片快轴的夹角θ为±45º时,合成光矢量末端的运动轨迹为一个正圆,即出射光为左旋/右旋圆偏振光。
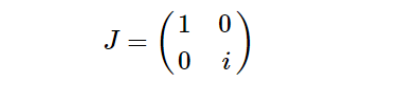
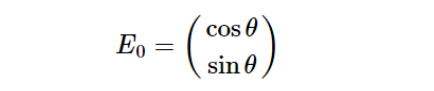
经过四分之一波片后,出射光E1:
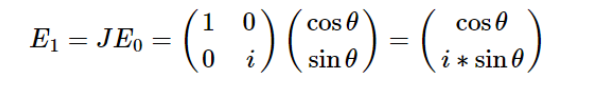
显然,上式代表的是一个椭圆偏振光。 特别地,当θ为+45º时,E1为左旋圆偏振光,当θ为-45º时,E1为右旋圆偏振光。
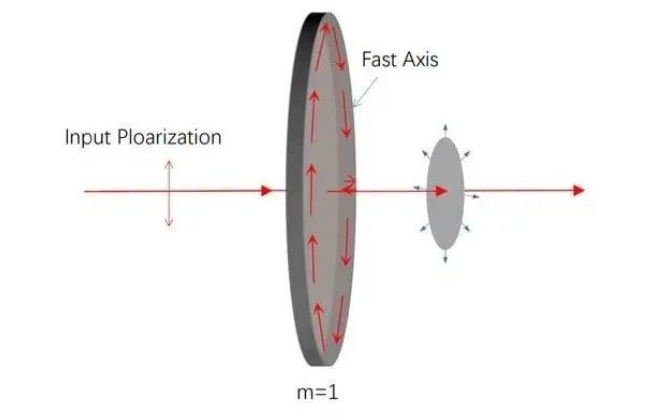
图11.涡旋波片(m=1)。
根据入射光偏振态的不同,涡旋波片可以产生涡旋光束或矢量偏振光束,具有广泛的应用前景。 例如涡旋光束是一种具有螺旋形相位波前、中心具有相位奇点的新型光束。 由于相位奇点的存在,涡旋光束中心处光强为零,在聚焦面上呈暗中空的环形强度分布。 利用涡旋的特殊性质可以发展光镊技术,可以实现对微粒的捕获; 其携带的轨道角动量能操控粒子旋转,这种技术被称为光学扳手; 涡旋光束的拓扑荷数取值的任意性使得人们可以利用轨道角动量来实现高维度信息的编码,显著提高信息容量和安全。 如图12、13,分别是一种典型的涡旋光束: 拉盖尔-高斯光束的三维光强分布和涡旋光束的螺旋相位波前。
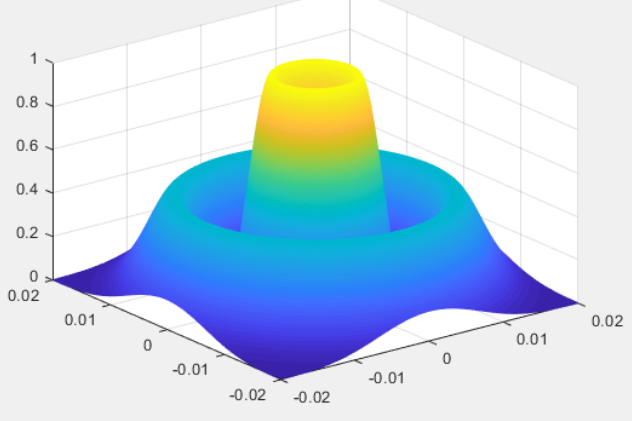
图12.l=1,p=1的拉盖尔高斯光束三维光强分布。

图13.拓扑荷数为1的涡旋光束螺旋波前。
涡旋波片是一种偏振相关的PB相位元件,它对入射光束产生的相位调制依赖于入射光的偏振态。 可以通过琼斯矩阵计算的方法说明涡旋波片产生涡旋光束和矢量偏振光束的过程。
涡旋波片的琼斯矩阵可以表示为:
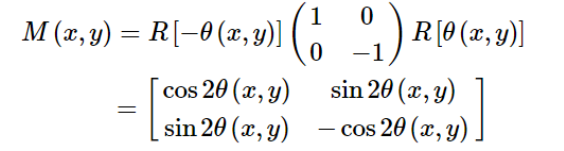
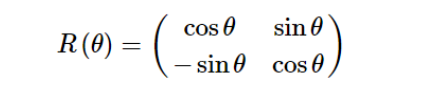

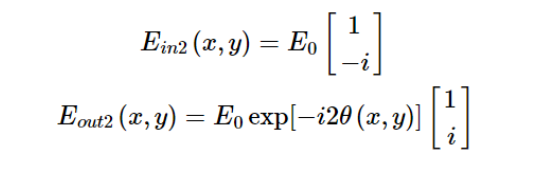
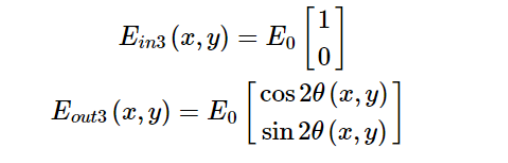
本文由“壹伴编辑器”提供技术支持