LBTEK光学研发团队致力于为广大科研、工业客户提供优质的产品和服务。 团队成员全部是硕士以上学历,其中20%具有博士学历,团队成员来自国内外知名企业及高校,深耕科研和工业行业多年,具备扎实的光学理论基础,及仿真算法、生产工艺、实验系统设计和集成器件开发经验。
为了在数学上定量地表示偏振光,可以巧妙地利用琼斯矢量和斯托克斯矢量,对光波的偏振态和偏振器件对偏振光的作用特性进行简练的矩阵式表达。 其中琼斯矢量只跟光波的振幅和相位相关,相应的琼斯矩阵为 2×2 阶矩阵,仅适用于表示偏振光; 斯托克斯矢量与光波的强度相关,相应的穆勒矩阵为4×4阶矩阵,适用于表示偏振光、部分偏振光和自然光。 下面我们将分别阐述琼斯矢量、琼斯矩阵、斯托克斯矢量、穆勒矩阵。
琼斯矢量
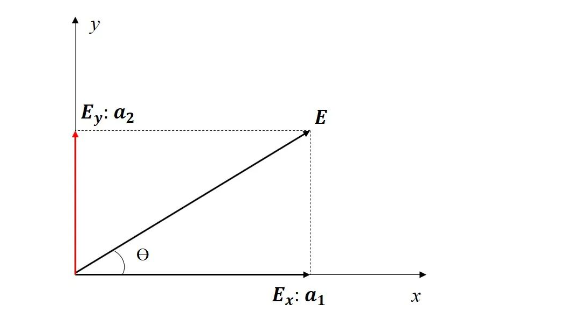
图1.光矢量的分解。
如图1,将偏振光E分解为沿x方向和沿y方向正交的 两个偏振分量 :
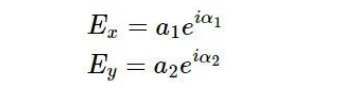
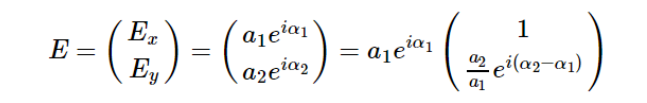
E的光强等于两个正交分量的强度之和:

因此可以偏振琼斯矢量可以归一化写为(矩阵下方为(a2/a1)e^(iδ)):
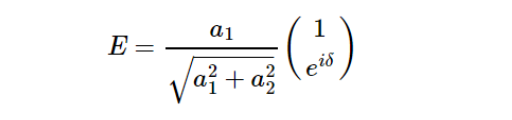
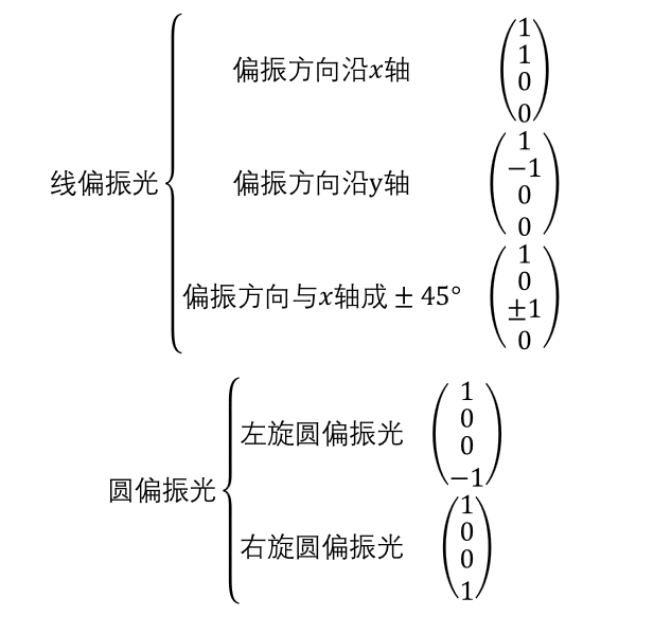
式中δ为两个正交偏振分量间的相位差。 根据上式,易得出典型偏振光的归一化琼斯矢量:
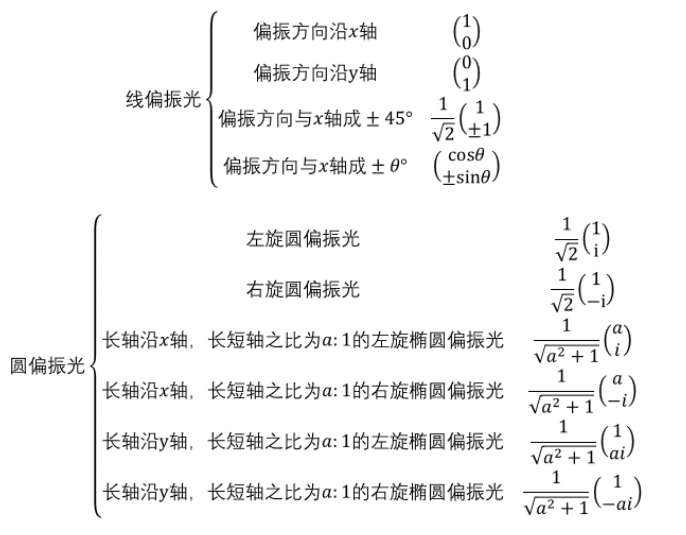
上面给出了典型线偏振光和圆偏振光的归一化琼斯矢量,通过琼斯矢量的矩阵加减运算,易求出多个偏振光线性叠加后的偏振态。 设任意两个偏振光的琼斯矩阵表示为:

如果E1、E2满足关系:
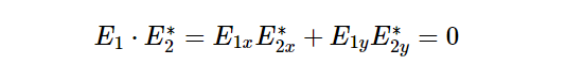
则表示 E 1 、 E 2 光是一对正交偏振态,*表示复数共轭。 任何一种偏振态都可以用一对特定正交偏振态的两个琼斯矢量的线性组合来表示。 例如,任意偏振光可以分解为水平方向偏振和垂直方向偏振的一对正交线偏振光的线性组合,也可以分解为一对正交的右旋圆偏振光和左旋圆偏振光的线性组合,这里不再赘述。
琼斯矩阵
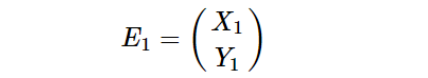
经过某偏振器件后变为:
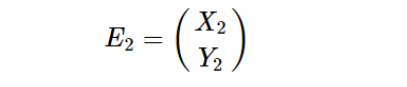
那么可以用一个2×2阶矩阵来表示偏振器件的线性变换作用:
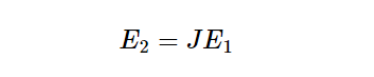
即:
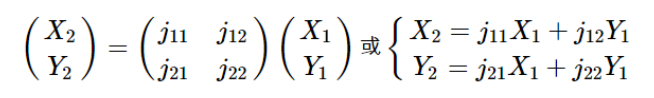
称矩阵:
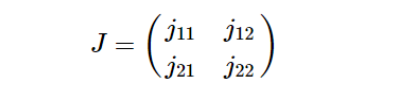
下面举例说明偏振器件琼斯矩阵的求解过程。
线性偏振器的琼斯矩阵
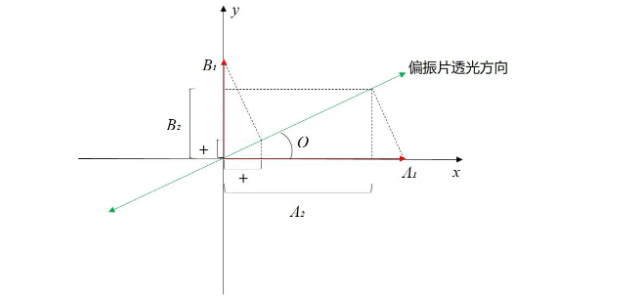
图2.线性偏振器的琼斯矩阵推导。
如图 2,在x-y坐标系中, 线性偏振器的透光方向 与x轴成θ角。 入射光在 x 轴和y轴 上的分量分别为 A1 、B1。 A1、B1沿线性偏振片的透光方向上的投影分量可以透过偏振片,分别为A1cosθ、B1sinθ,即出射光为A1cosθ+B1sinθ。 将出射光再投影到x轴和y轴上,得到出射光的两个偏振分量A2、B2:
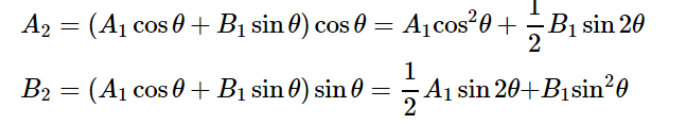
写成矩阵形式为:
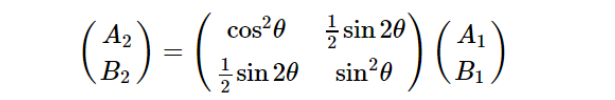
由上式可知,线性偏振器的琼斯矩阵为:
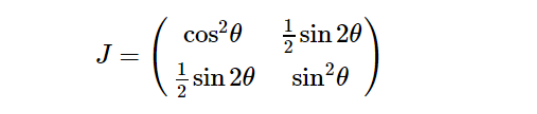
波片的琼斯矩阵
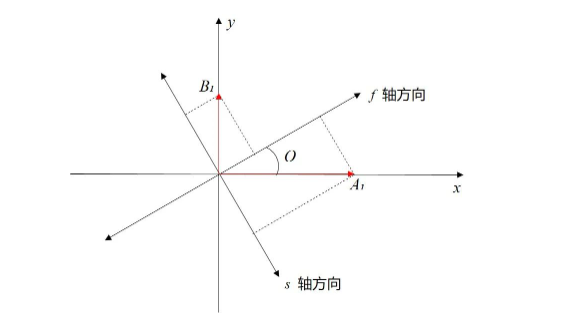
图3.波片的琼斯矩阵推导。
如图3, x-y坐标系中,波片的快轴方向与x轴成θ角,对入射光产生的相位延迟量 大小为 δ , 入射光在 x 轴和 y 轴上的分量分别为 A1 、B1 ,将这两个分量分解到波片的快轴、慢轴上:
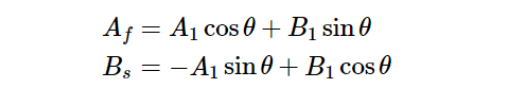
用矩阵表示为:
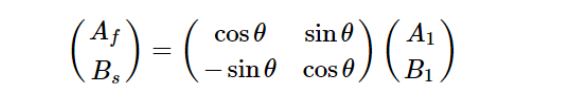
入射光经过波片出射时,快、慢轴方向上的偏振分量存在一个相对的相位延迟量:

用矩阵表示为:
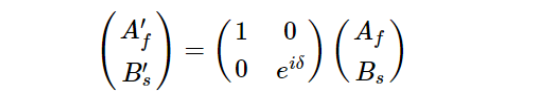
将出射光在快、慢轴上的分量再分别投影到 x 轴和y轴上,得到出射光琼斯矢量在x轴和y轴上的分量:
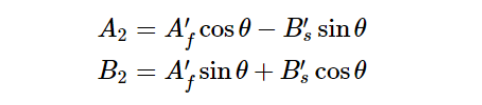
用矩阵表示为:
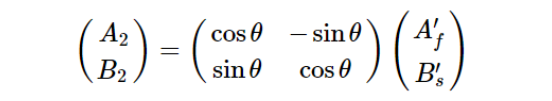
依次代入各偏振分量,有:
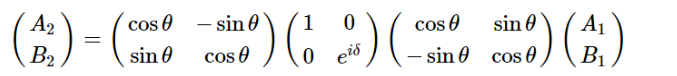
经过计算整理,得到波片的琼斯矩阵:
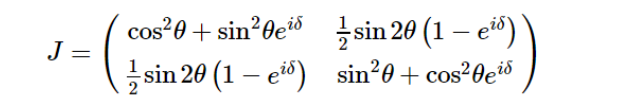
或:

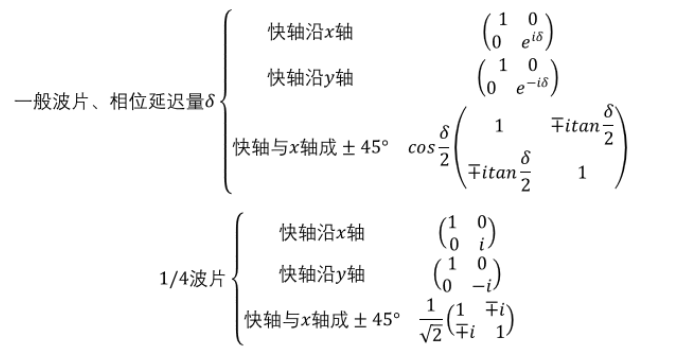
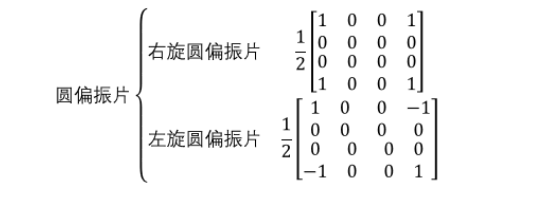
根据上述方法,可以推导出典型偏振器件的琼斯矩阵:


斯托克斯矢量
琼斯矢量能够很好地描述光的偏振状态,形式极为简洁,但是只适用于表示线偏振光和圆偏振光。 在琼斯矢量出现之前,斯托克斯就提出了四个参量,用于表示偏振光,这就是斯托克斯矢量:


根据S0、S1、S2、S3代表的物理意义,可以得出典型偏振光的归一化斯托克斯矢量:
假设两束不相干的单色光(S0’、S1’、S2’、S3’)、(S0”、S1”、S2”、S3”)在空间中某个区域叠加,合成波斯托克斯矢量的任意参量就是两束光对应的参量之和,即合成波的斯托克斯矢量为: (S0’+S0”、S1’+S1”、S2’+S2”、S3’+S3”)。
结合偏振光学第一讲“理解偏振光”的内容,不难得出以下结论:
偏振椭圆长轴方位角φ满足:

椭圆度ε满足:
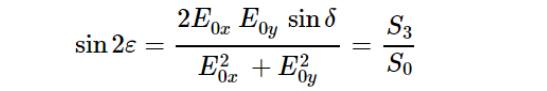
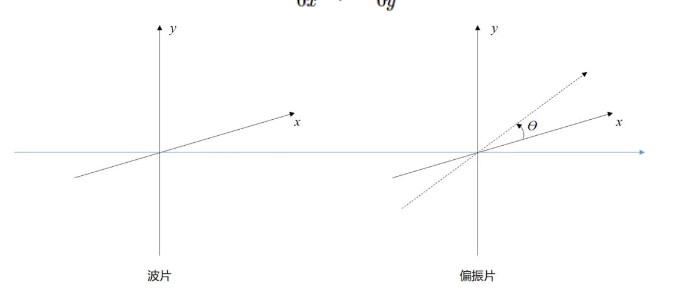
图4.斯托克斯矢量的测量。
由于斯托克斯参量都是是用光强度公式来表示的,因此可以直接测量。 斯托克斯参量的测量通常采用旋转波片/偏振片法。 如图4,入射光依次经过波片、线偏振片之后出射。 入射光 沿 x、y轴的分量可以表示为:
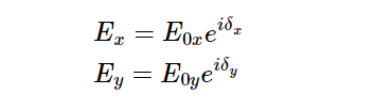
用斯托克斯矢量可以表示为:
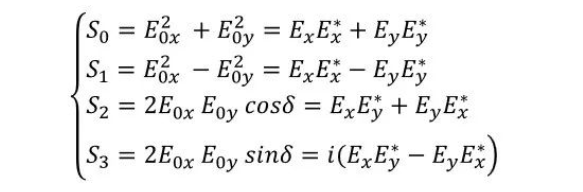
假设波片快、慢轴分别沿x方向和y方向,入射光经过波片之后,光沿x、y轴的分量产生Φ的相位差,为方便计算,假定x轴分量超前 Φ /2的相位,y轴分量滞后Φ/2的相位:

线偏振片初始偏振透过方向为沿x轴,旋转偏振片,使得偏振透过方向与x轴成θ角,透过偏振片出射的光为:
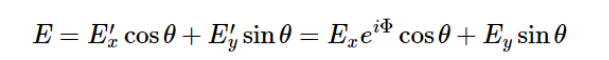
出射光光强为:

代入E的表达式,有:
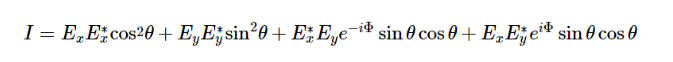
利用三角函数公式,可以将I写为:
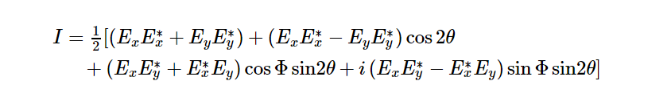
用斯托克斯矢量表示为:

显然,当入射光确定后,出射光强I是关于Φ、θ的函数,用I(Φ,θ)表示:
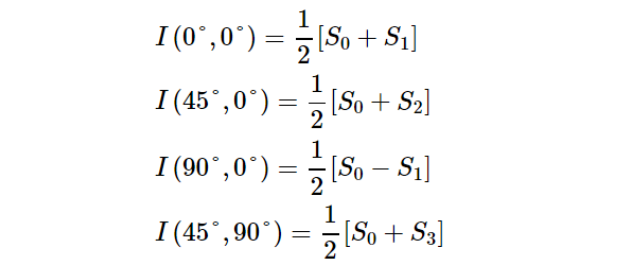
解上述方程,可以得出斯托克斯矢量:
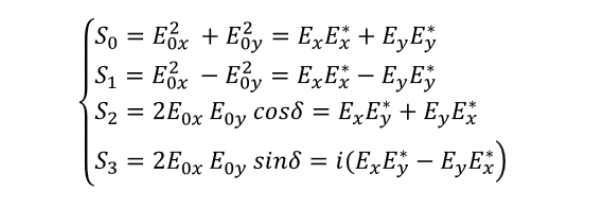
穆勒矩阵
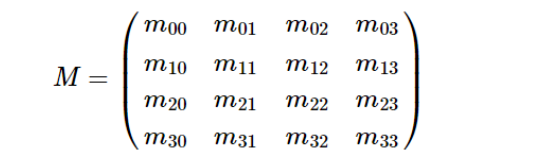
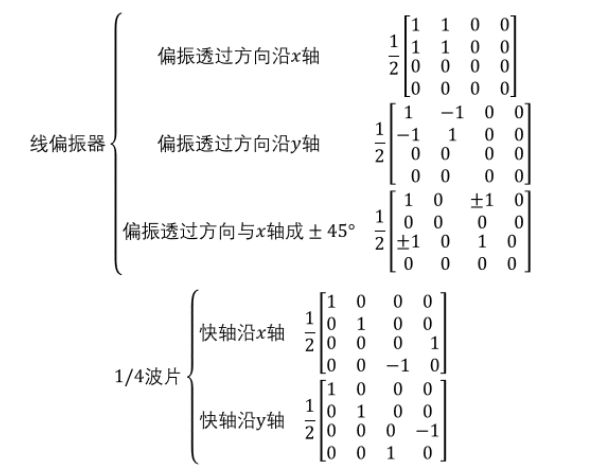
下一讲,偏振器件综述,敬请期待~