搭建光学系统时，杂散光的存在对实验造成影响。 杂散光的来源多种多样，光学元件表面的反射是其中的一种。 增透膜（减反射膜）的功能是减少光学元件表面的反射光，从而增加光学元件的透过率，以减少系统的杂散光。

能量守恒定理： 能量既不会凭空产生，也不会凭空消失，它只会从一种形式转化为另一种形式，或者从一个物体转移到其它物体，而能量的总量保持不变。

光束入射到增透膜时，在膜层表面发生反射，穿过膜层后在基底表面再次发生反射，而后经膜层表面折射出射。 当两次反射光的光程差为半波长的奇数倍时，两束光干涉相消，合振幅最小，从而减少了反射。 当一束光携带能量E₀入射到镀有增透膜的光学元件表面, 在光学元件表面会发生能量转换，反射光总能量为E_R，透射光总能量为E_T，不考虑吸收、散射等因素，按照能量守恒定理，则有E₀=E_R+E_T，控制膜层参数使得整体E_R减少，则E_T增加，表征现象即为反射率降低，透射率增加。

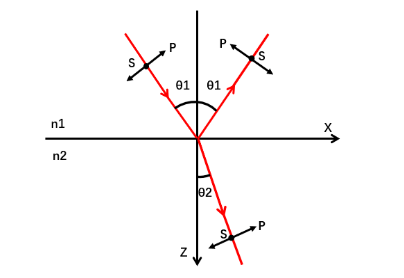
光波可以分为S波（垂直入射面）和P波（平行入射面）， 其反射和折射的振幅不同，根据菲涅尔公式，可以得到S光、P光反射率及透射率公式如下：

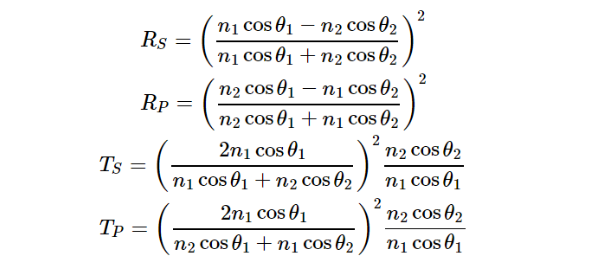
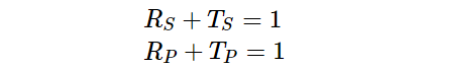
θ表示入射角度，当θ₁=θ₂=0°时，表示正入射，有：

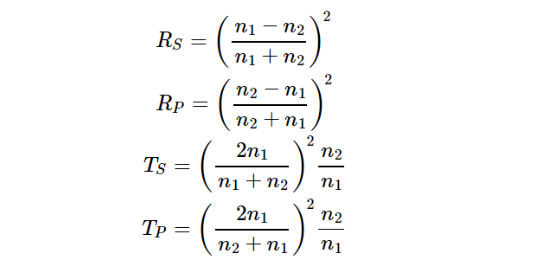
根据菲涅尔公式，光从空气中入射到基底，当n₁=1，n₂=1.5时，可以得到如图2所示的反射率与入射角度的关系曲线。 在没有镀增透膜且正入射的情况下，R_S、R_P为4%左右，随着入射角度增大，R_S、R_P会有差异，当θ角度为56.3°时R_P几乎为0，表示P光全部折射，只有S光有反射，该角度定义为布儒斯特角。

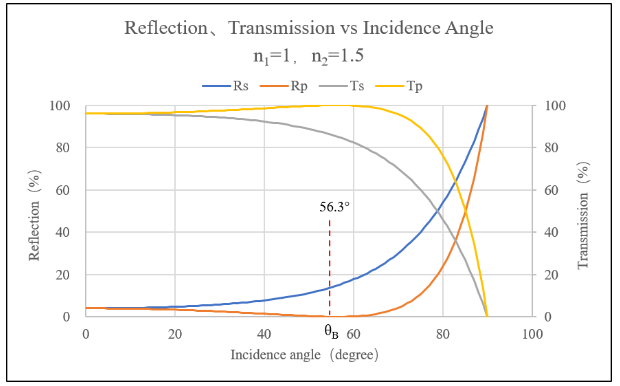
图2.S光、P光反射率、透过率 vs 入射角度

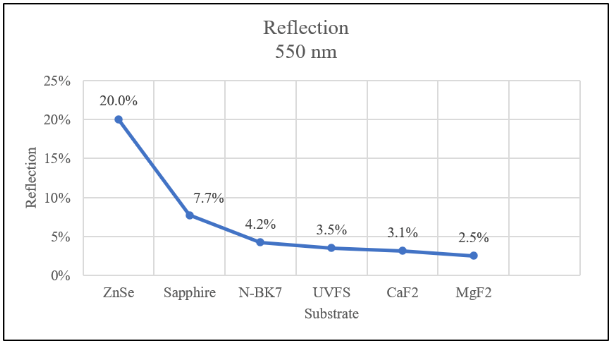
图3.反射率 vs 基片（从空气中入射，n₁=1）

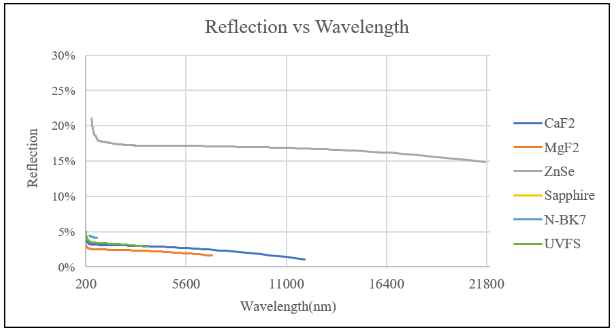
图4.不同基底材质表面反射率 vs 波长

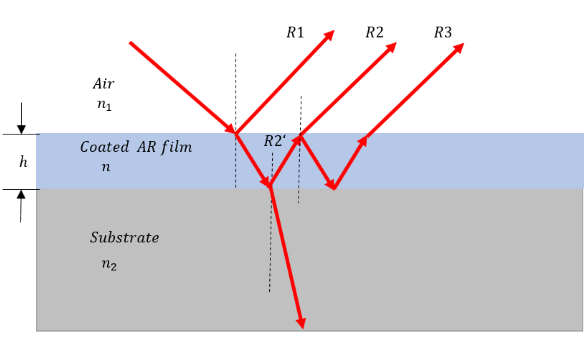
图5.光在增透膜层中反射与折射示意图

如图5所示，光束从空气入射到镀有增透膜的基底，空气折射率为n₁，在折射率为n₂的基底上镀上折射率为n的薄膜，厚度为h，考虑小角度入射时（正入射）， 空气与薄膜表面反射率R_1，透射率为1-R₁：

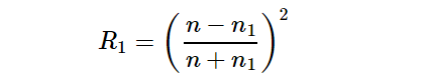
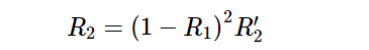
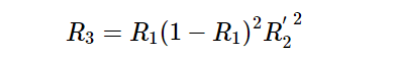
理想情况下如果能实现R₁=R₂, 且相位相差π，则可以完美消除反射光。

当R₁=R₂，即有：

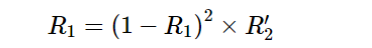
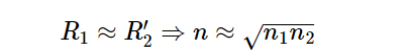
对于空气n₁=1，常规玻璃n₂=1.5的典型情况，可得n=1.22，但市面上还找不到这种折射率材料，通常用n=1.37的MgF₂作为增透材料. 此时，反射率可降低到1.22%左右。

由R₁、R₂光程差引起的相位差为：

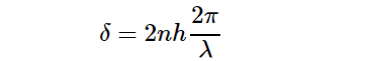
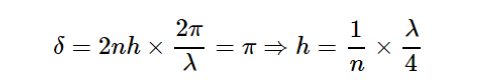
综上，可以得出理想情况下完美消除反射光的膜层参数：

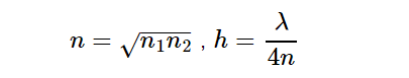
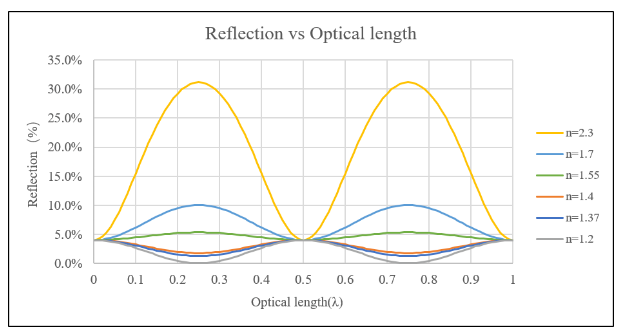
在550 nm波长处，当采用不同增透膜材料（折射率n不同）时，反射率与增透膜光学厚度的关系曲线如图6所示（空气折射率n₁=1，基底折射率n₂=1.5，正入射）。

• 当n<n₂，膜层起增透的作用，且当膜层光学厚度(nh)为λ/4的奇数倍时，R₁、R₂的相位差δ为π的奇数倍，此时可得到最低的反射率。 膜层折射率n越小，反射率越低。

• 当n>n₂时，膜层起增反的作用，且当膜层光学厚度为λ/4的奇数倍时，反射率最高。 膜层折射率n越大，反射率越高。
• 当膜层光学厚度是λ/4的偶数倍时，不起增透作用。

常见的V型增透膜（单波长反射率曲线成V型）采用双层膜设计，在设计波长处，反射率最低，当工作波长远离设计波长时，其反射率快速增加，增透效果可能比单层膜时更差。 宽谱W型增透膜为了优化波段范围，采用双层膜设计，第一层与空气接触的膜层 光学厚度为λ/4的奇数倍 ，而第二层与基底接触的膜层 光学厚度 为λ/2的奇数倍。 两者反射率曲线见图7。

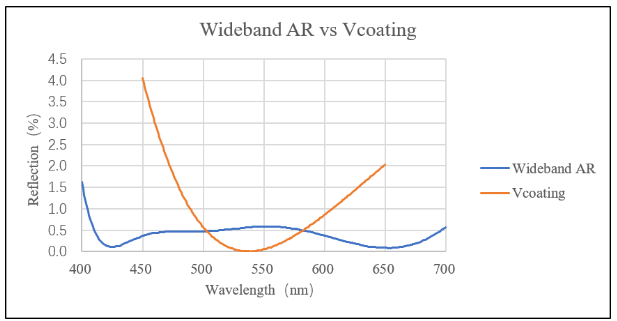
图7.宽谱增透膜 vs V型增透膜