技术中心

量子系列（三）：量子态光场—纠缠态

发布时间：2022-06-08 00:00:00 阅读次数：552

纠缠（entanglement）是量子力学最吸引人的特征之一，在量子信息中扮演着极其重要的角色。量子纠缠反映了量子体系中子系统之间的相关性与不可分性。以两个向相反方向移动但速率相同的纠缠粒子为例，即使一个行至太阳边，一个行至冥王星边，在如此遥远的距离下，它们仍保有关联性：当其中一个被操作（例如量子测量）而状态发生变化，另一个也会即时发生相应的状态变化。如此现象导致了“超距作用”的猜疑，仿佛两个粒子拥有超光速的秘密通信一般，与狭义相对论中所谓的定域性原理相违背，被爱因斯坦描述为“鬼魅般的超距作用”。目前，量子纠缠已经被广泛应用到多个方面，如量子密码，量子密钥分发，量子隐形传态，量子计量，和引力波探测器等。

我们考虑由两个相异物理系统组成的复合系统，按量子力学第四公设，复合物理系统的状态空间是分物理系统状态空间的张量积，若将分系统编号为

到

，系统

的状态被置为

，则整个系统的状态可以表述为

。具有精确已知状态的，即可以用一个态矢表述的量子系统称为纯态（purestate）系统，两体纯态就是指能用单一波函数描述的两体态。就两体系统而言，它可以表示成：

与此相反，如果一个量子系统是由若干不同态矢

，

描述的子系统构成，每个子系统在该系统中以确定的概率出现，则称这个系统为混合系综。混合系综的状态称为混态（mixedstate）。换言之，若干个纯态的非相干混合构成了混态。这些纯态之间不存在相干叠加及发生干涉的问题。

上面提到两体系统的纯态在此基础上可以区分成两大类：可离散态和纠缠态。要定义可离散态和纠缠态的概念，先来了解一下复合系统纯态的Schmidt分解。可以证明，总能将复合系统AB的任一纯态

表示为如下标准的Schmidt分解形式（或称Schmidt极化形式）：

其中，

、

分别是A和B中的某两组特殊的正交基。两体复合系统的任一纯态

的Schmidt分解式中的项数称为Schmidt数。于是定义可离散态和纠缠态如下：

可离散态：两个子系统构成的复合系统纯态的展开式的项数等于，A和B处于确定态，就称是非纠缠的（或是可离散的），即可离散态是两个子系统的纯态的直积态。
纠缠态：复合系统的一个纯态，如果不能写成两个子系统纯态的直积态，即Schmidt分解的展开式中含有多项，这个态就称为纠缠态，其中子系统A和B则是相互纠缠的，不可分的，即使它们空间离散，对A的观察也必然会影响B的测量结果。

根据量子系统的本征态具有离散谱还是连续谱，量子纠缠可以分为两大类：离散变量纠缠和连续变量纠缠。

如存在于电子之间的自旋纠缠，单光子之间的偏振纠缠、动量纠缠、能量－时间纠缠等，都属于离散变量纠缠。这种纠缠具有对损耗不敏感等特点，可用于完成高保真度的量子通信。
如光场正交分量之间的纠缠，粒子的位置动量之间的纠缠等，都属于连续变量纠缠。这种纠缠具有探测效率高，频率带宽大，且产生的纠缠态拥有无条件和确定性等特点。

二粒子系统的纠缠概念最早于1935年在Einstein，Podolsky和Rosen（EPR）三位科学家联合发表的著名论文中提出，因此由二个子系统构成的纠缠态常常又被称为“EPR”对。虽然在原始文献中所讨论的可观测量子变量是具有连续谱的正交坐标与动量，但由于难以在量子水平上精确测定微观粒子的坐标与动量，所以早期验证纠缠的实验都是用离散变量粒子自旋或光子的偏振执行的。多组份纠缠态是相对于两组份纠缠态而言的，它是指纠缠由多于两个的子系统共享，这是研究量子通讯网络和量子计算的基础。多组份纠缠态形式很多，目前已经研究的主要包括两大类GHZ纠缠态和Cluster纠缠态。

离散变量纠缠的研究取得了令人瞩目的成绩，目前己经利用它完成了量子离物传态、量子密集编码、纠缠交换等重要的量子信息实验。实验上已经产生了三光子、四光子、五光子GHZ纠缠态以及四光子Cluster纠缠态。中国科技大学潘建伟研究组实验产生了六光子GHZ纠缠态和Cluster纠缠态。然而由于这些实验都是利用自发参量下转换，所以纠缠光子对的产生是几率性的。目前正在探索新型的单光子源，预计随着将来腔量子电动力学的发展，实验上有望得到决定性而非几率性的单光子源以及纠缠光子对。

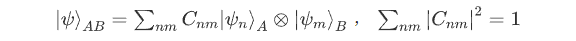
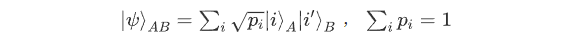
从1972年S.Freed-man等人利用Ca原子能级跃迁产生纠缠光子对开始，此后不同种类的离散变量量子纠缠态光源逐步得到了实验研究，包括偏振纠缠态、时间纠缠、时间模式纠缠以及空间模式纠缠等。作为量子信息载体的光子，具有与环境相互作用比较弱，消相干比较小，光子偏振易于控制等明显优势，光子系统的量子纠缠在实际量子信息处理过程中更具有优越性。在线性光学系统中，光子纠缠态的制备一般是利用自发参量下转换过程（SPDC），比如，利用激光泵浦特殊切割角度的非线性光学晶体（BBO），来产生双光子偏振纠缠态。

图1 双光子偏振纠缠态的制备方法

连续变量方面，虽然实验研究相比离散变量方面略有滞后，但也取得了很大的成绩。连续变量EPR纠缠由H.J.Kimble研究组于1992年首次获得，通常指的是基于光场正交振幅和正交相位分量的纠缠态，他们在非简并参量放大过程中产生双模压缩态光场，并证明了光场的量子相关性。根据海森堡不确定关系可知，我们无法同时对正交振幅和正交相位算符进行精确的测量。而对于两束光的正交振幅和和正交相位差，或者正交振幅差和正交相位和，它们之间满足对易关系，是可以实现同时精确测量。

对于理想的连续变量EPR纠缠,其正交振幅和正交相位之间的关系满足下列公式：