我们知道光是一种电磁波，经典光场在自由空间的传播特性，可以通过麦克斯韦方程组来描述,而光场的量子特性，则需要引入湮灭算符和产生算符来进一步描述，其都为非厄米算符，属不可观测量。但是，产生和湮灭算符也可以表示成可观测量的形式： 

其中和分别为电磁场的正交振幅算符和正交位相算符，属可观测量。在量子光学实验中，这两个物理量也常用于描述光场量子态的物理量。

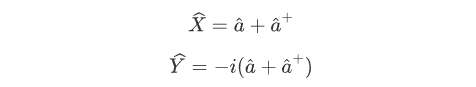
根据产生算符和湮灭算符的对易关系，可以得到光场的正交振幅算符和正交位相算符之间也满足对易关系： 

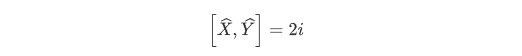
根据海森堡不确定性关系可知，光场的正交振幅算符和正交位相算符满足不确定关系： 

其中，和分别表示正交振幅算符和正交位相算符的标准方差：

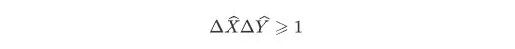
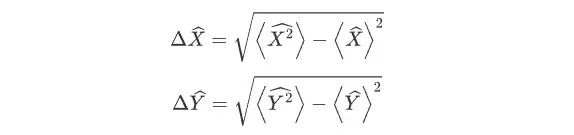
不确定关系式表明，我们无法同时对电磁场的正交振幅算符和正交位相算符进行精确的测量。当光场的正交振幅正交位相满足 =1 时，则称之为最小不确定态。

下面我们介绍几种常用到的量子态光场，包括相干态、压缩态及其在光子数态中的表示。

(b) 正交振幅压缩真空态（蓝）及压缩相干态（橙）

• 对于真空态来说，其平均光子数为零，但是其量子噪声起伏（方差）不为零，而对于相干态来讲，其平均光子数不为零，体现在相空间中为虚线所示长度，其物理描述为相干态的本征值，也可以理解为单模光场的复振幅，同样其量子噪声起伏不为零。

• 图1b所示为正交振幅压缩真空态（蓝）与正交振幅压缩相干态（橙），与图1a相比，其某一正交分量的量子噪声起伏（方差项）小于真空态和相干态的，称为该分量压缩，而对应的另一分量必定大于真空态和相干态的量子噪声起伏，被称为反压缩，这就是压缩名字的由来。

光子数算符和单模电磁场的哈密顿算符相互对易，因此两者有共同的本征态，这个共同的本征态就是光子数态，用光子数标记状态，此时光子数算符的本征方程为：

当时，光子数态变为真空态 。

引入正交分量算符： 

利用上式及对易关系，计算可得，在光子数态中正交分量和的平均值和方差分别为 

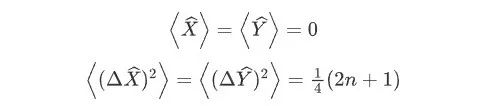
对于真空态，即时， 

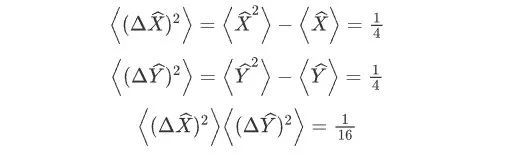
满足最小的不确定关系，所以真空态是最小不确定态，其量子涨落称为量子噪声极限。

与真空态相同，相干态也是最小的不确定态，在1963年，由Glauber等人提出，自此相干态便在量子光学实验中被广泛应用。在薛定谔表象中，光场湮灭算符的本征态就是相干态，表示为：

复数为相干态的本征值，可以理解为单模光场的复振幅。与真空态不同，相干态是有平均光子数的，其在光子数表象下可以表示为

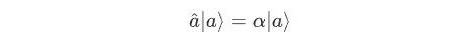
相干态的平均光子数，并且其分布满足泊松分布。

此外，相干态可以通过将真空态平移产生： 

其中，表示平移算符。

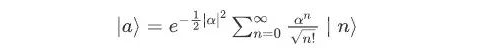
在相干态中计算正交分量和的平均值和方差： 

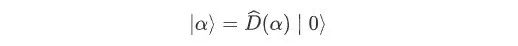
可得，在相干态中正交分量和的平均值与复振幅有关，而量子涨落与的取值无关。通常将相干光的量子噪声起伏（方差）称为散粒噪声基准。

压缩态有着与相干态不同的量子噪声特性：其一个正交分量噪声起伏小于真空噪声起伏，因此，压缩态自诞生之初就被用于提高量子测量精度。

压缩态的性质可以通过压缩算符来推导，将压缩算符定义为

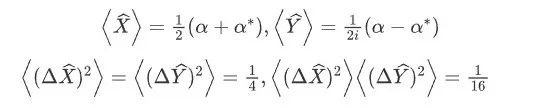
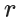其中压缩算符，为压缩因子，表示压缩度的大小；为压缩角，用来描述相空间中压缩的方向，取值范围为  。

将压缩算符作用在真空态上可获得压缩真空态，而作用在相干态可获得压缩相干态：

对于压缩真空态，其平均光子数和光子数方差分别为：

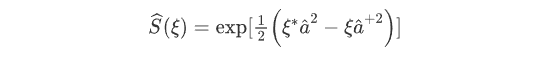
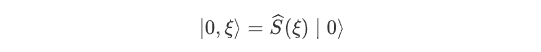
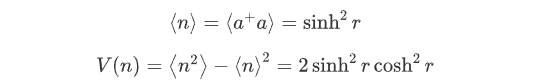
电磁场正交算符和的平均值和方差分别为 

其中，为压缩角，用来描述压缩方向。特别地，当=0时，

对于压缩相干态，其平均光子数为： 

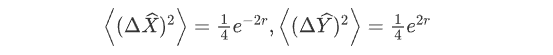
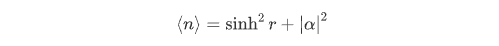
在压缩相干态中，为了更好地描述一般方向的压缩，引入下列旋转正交分量： 

计算可得，在压缩真空态中，算符和的平均值和方差分别为：

我们可以看到压缩相干态的噪声起伏（方差）和压缩真空态的相同，而平移算符只改变正交算符和在量子态中的平均值，而不改变其方差（量子涨落），所以压缩相干态的标准差与压缩真空态的相同。

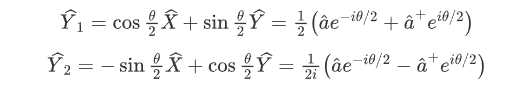
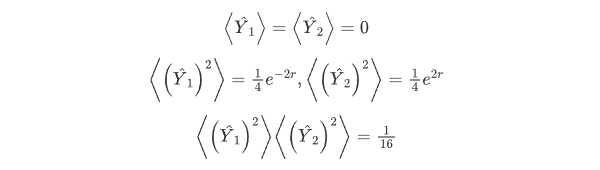
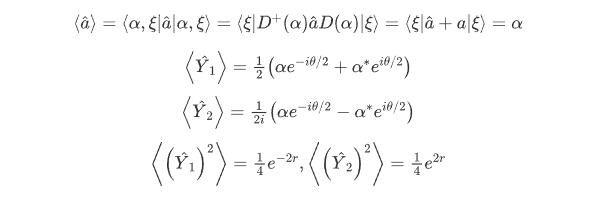
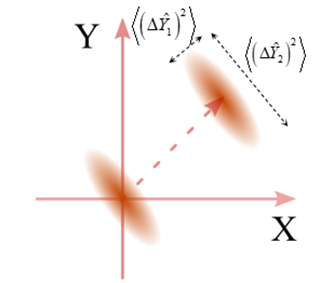
图2 压缩真空态（原点位置）和压缩相干态在相空间分布图

参考文献：

[1]郭光灿. 量子光学[M]. 高等教育出版社, 1990.

[2]张智明. 量子光学[M]. 科学出版社, 2017.