辐射度学是一门研究各种电磁辐射强弱及其测定的学科，它包含辐射体本身向不同方向辐射能力强弱的研究，以及被辐射物体的表面接收能量情况研究，辐射过程代表了客观存在的能量，其基本单位为瓦（\( w \) ）或者焦耳（\( J \) ）。

在研究辐射度学的过程中，为了更直观的表述辐射过程定义了辐射能、辐射功率（辐射能通量）、辐射强度、辐射亮度、辐射照度等度量参数。下面对相关参数进行介绍。

辐射能是辐射度学最基本的一个量，定义为以辐射形式发射或传输的电磁波能量，用字母\( Q \) 表示，单位为焦耳（\( J \) ）。常用公式\( Q=hv=\frac{hc}{\lambda} \) 计算单光子能量。其中\( h \) ： 普朗克常量；\( v \) ： 光的频率；\( c \) ： 真空中光速；\( \lambda \) ： 光的波长。

辐射功率是指单位时间内辐射源发出或通过一定接收截面的辐射能 ，用字母\( Φ \) 表示，单位为瓦（\( w \) ），它与辐射能的关系为：\( Φ=\frac{Q}{t} \) 。

辐射照度的定义不是针对辐射源，而是针对辐射接收面来制定，它表示辐射源辐射到单位接收面面积上的辐射功率。常用字母\( E \) 表示，单位为\( W/cm^{2} \) 。常用来测量辐射源的各类光电器件，比如光功率计、光电管、光纤光谱仪等，其直接测量值都是探测面的辐射照度，以点光源产生的照度为例，其示意图如下。

其关系式为\( E=\frac{Φ}{s} \) ，\( S \) ：辐射接收面的面积；\( Φ \) ：点光源在辐射接收面上的辐射通量。

辐射强度用字母\( I \) 表示，它是在点辐射源的基础上进行定义，即当辐射源的线度足够小或探测距离足够远时，将辐射源称为点源（根据GB/T 26184-2010，当探测距离是辐射源线度的5倍以上时，辐射源可当作点源处理）。 点源\( Q \) 沿某一方向\( r \) 的辐射强度定义为沿此方向上单位立体角内发出的辐射功率。

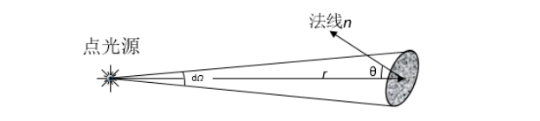
图2 点光源辐射强度示意图

如图2所示，以\( r \) 为轴取一立体角\( dΩ \) ，设\( dΩ \) 内的辐射功率为\( Φ \) ，则沿\( r \) 方向的辐射强度可表示为：\( I=\frac{Φ\cdot r^{2}}{S\cdot cos\theta}=\frac{E\cdot r^{2}}{cos\theta} \) ，其中\( r \) ： 辐射接收面到辐射源的距离；\( S \) ：辐射接收面的面积 ；\( \theta \) ： 辐射接收面法向与\( r \) 的夹角。 由此公式可知，当辐射源一定时，其在某接收面上的辐射照度与距离的平方成反比关系，这就是被大家熟知的平方反比律。

当使用各类光电器件测量辐射源的辐射强度时，经过标定的光电器件可直接获取接收面处的辐射照度，再测量出辐射接收面到辐射源的距离\( r \) ，即可通过此公式计算出辐射源的辐射强度，但在测试过程中有如下几个注意事项：

（1）探测面的法向必须与辐射发射方向重合，否则探测面需要考虑投影面积，即公式中的\( cos\theta \) ；

（2）辐射强度的定义是建立在辐射点源的基础上，所以探测距离必须是辐射源线度的 5 倍以上，但由于 辐射照度与 距离的平方成反比关系，造成接收面处的辐射照度往往较弱，选择测量器件时尽量选择灵敏度高和探测面大的器件。

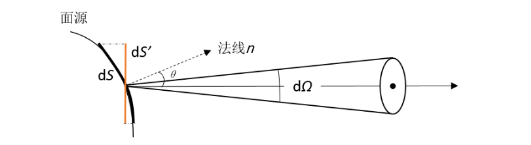
辐射强度是针对点辐射源而定义，但在实际中多数情况里，我们看到的辐射源有一定的辐射面积，这种辐射源叫面源。面源表面的每块面元\( dS \) 沿某方向\( r \) 有一定的辐射强度\( I \) ，如图3所示，设\( r \) 与法线\( n \) 的夹角为\( \theta \) ，当迎着\( r \) 的方向探测\( dS \) 时，面元\( dS \) 的投影面积为\( dScos\theta \) ，所以面元\( dScos\theta \) 沿\( r \) 方向上的辐射亮度定义为在此方向上单位投影面积的辐射强度，或者表述为沿\( r \) 方向上从单位投影面积在单位立体角内发出的光功率，辐射亮度常用字母\( B \) 表示，其表达公式为：\( B=\frac{I}{S\cdot cos\theta}=\frac{Φ}{\Omega\cdot S\cdot cos\theta} \) 。

在使用成像系统的过程中人们往往笼统的讨论成像的亮暗，其实这里存在像的亮度和像的照度的差异。当用助视光学仪器（比如显微镜）观测物体时，光学仪器所成的像是人眼睛观测的对象，而眼睛只接收一定立体角内的光通量，因此这是像的亮度问题。

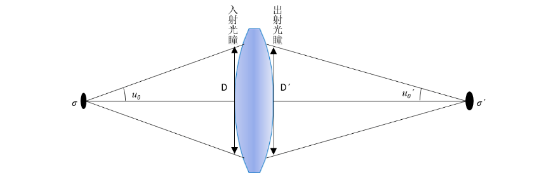
如图4所示，设 \( y、\sigma、B、u_{0}、n、l \) 分别为傍轴小物的线度、面积、亮度、入射孔径角、物方折射率和物距，\( y^{'}、\sigma^{'}、B^{'}、u_{0}^{'}、n^{'}、l^{'} \) 为像方的相应量，为了简化推导的过程，设σ沿各方向的辐射强度一致（朗伯辐射体），则可根据公式\( Φ=B\cdot \sigma\cdot \frac{\frac{\pi D^{2}}{4}}{l^{2}}=\pi B\sigma sin^{2}u_{0} \) 计算出进入入射光瞳的辐射通量 ，同理，射出出射光瞳的辐射通量可表示为：\( Φ^{'}=B^{'}\cdot \sigma^{'}\cdot \frac{\frac{\pi D^{'2}}{4}}{l^{'2}}=\pi B^{'}\sigma^{'} sin^{2}u^{'}_{0} \)

假设我们不考虑光通过成像系统的损耗，即\( Φ=Φ^{'} \) ，则可得到：\( \frac{B^{'}}{B}=\frac{\sigma sin^{2}u_{0}}{\sigma^{'} sin^{2}u^{'}_{0}} \) ，而 根据阿贝尔正弦条件可知：\( nysinu_{0}=n^{'}y^{'}sinu^{'}_{0} \) ，将以上公式进行结合我们可以得到新的表示：\( \frac{B^{'}}{B}=\frac{\sigma}{\sigma^{'}}\times\frac{n^{'2}y^{'2}}{n^{2}y^{2}}=\frac{y^{2}}{y^{'2}}\times\frac{n^{'2}y^{'2}}{n^{2}y^{2}}=\frac{n^{'2}}{n^{2}} \) ， 以上就是光学成像系统像的亮度和物的亮度的关系，在物像两方的折射率相等时，若忽略光学系统对光的衰减，则像的亮度和物的亮度相等，这表明像的亮度与物像位置关系、系统放大率都无关，光学系统基本不改变像的亮度。

在使用相机拍照时，探测器感光程度的高低取决于投射到其每个像元上的总辐射功率大小，这实质上是一个关于像的照度的问题。

在图4中，如果在像面处放置光电探测器、光电探头或者光纤，则辐射接收面上的辐射照度可表示为：\( E=\frac{Φ^{'}}{\sigma^{'}}=\pi B^{'}sin^{2}u_{0}^{'}=\pi B\frac{n^{'2}}{n^{2}}sin^{2}u_{0}^{'} \) ， 对于傍轴系统有近似关系：\( sinu_{0}^{'}\approx\frac{n}{n^{'}}\cdot\left( \frac{D}{f} \right)^{2} \) ，所以辐射照度公式可变化为 \( E=\frac{\pi B}{4}\left(\frac{D}{f}\right)^{2} \) ， 此公式中\( D \) 与 \( f \) 之比就是光学系统的相对孔径，所以像的照度\( E \) 正比于相对孔径的平方，一般成像镜头上会标有\( F \) 数值 1 .4 ， 2 ， 2 .8 ， 4 ， 5 .6 ， 8 ， 1 1 ， 1 6 等，这就是镜头相对孔径的倒数，这序列中后一个数近似为前一个数的\( \sqrt{2} \) 倍，因此相对孔径按\( \frac{1}{\sqrt{2}} \) 的比值递减，从而探测器接收到的辐射照度依次减半。

由于常用来测量辐射源的各类光电器件，比如光功率计、光电管、光纤光谱仪等，经过校准后可直接测量探测面的辐射照度，所以在探测面之前加一个成像光学系统，再通过直接测得的照度数据和公式推算出面源的辐射亮度。