光,这种无处不在的电磁波,不仅照亮了我们的世界,还携带着丰富的物理信息。 光的偏振现象是一个热点话题, 而马吕斯定律是描述偏振光通过偏振片后光强度变化的定律。 本文将通过探讨马吕斯定律来揭示光的偏振特性。
光的偏振 : 基础概念
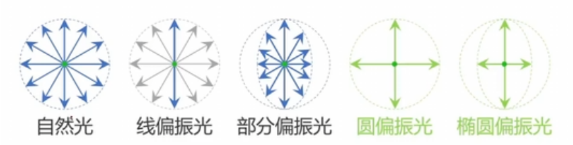
在自然光中,光波的振动方向是随机的,没有特定的方向性。 然而,当光波的振动被限制在一个平面内时,我们就说这束光是偏振的。 根据光的偏振特性,可以将光波分为线偏振光、部分偏振光、圆偏振光及椭圆偏振光。 偏振光的行为,可以通过马吕斯定律来描述。
马吕斯定律: 光的偏振与强度的关系
马吕斯指出: 强度为I0的线偏振光,透过检偏片后,透射光的强度(不考虑吸收)为 \( I_{2}=I_{1}cos^{2}\alpha \) 。 其中,α是入射线偏振光的光振动方向和偏振片偏振化方向之间的夹角。 当α=0°或180°时,\( I_{2}=I_{1} \) ,透射光最强。 当α=90°或270°时,I=0,透射光强为零。 当α取其他值时,光强介于0和I1之间。
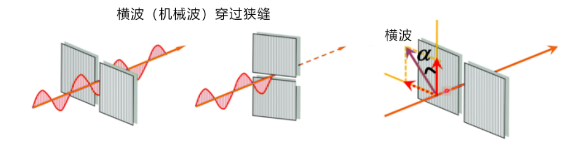
要想理解马吕斯定律,我们可以观察一下横波通过狭缝(狭缝代表横波的通过方向,即偏振化方向)时具有什么特征。 当狭缝的通过方向(偏振化方向)与横波的振动方向一致时,横波可以无阻碍的穿过狭缝进行传播; 当偏振化方向与横波的振动方向垂直时,横波无法通过; 当横波振动方向与偏振化方向成角度α时,只有振动的α角余弦分量可以通过。
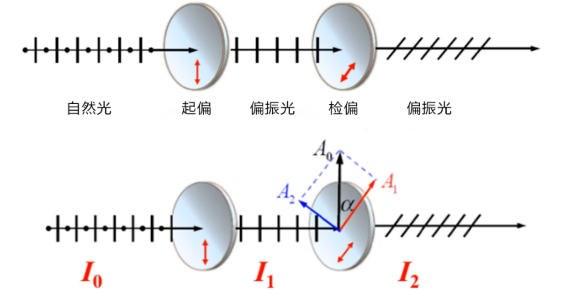
马吕斯定律的实验验证
当自然光入射时,自然光透过起偏器后成为沿竖直方向的线偏振光,且起偏器只允许自然光沿竖直方向的分量通过,因此可以得出, \( I_{1}=\frac{I_{0}}{2} \) 。
当线偏振光入射时,假设检偏器的偏振化方向夹角为α,线偏振光的振幅为A0,而检偏器只允许它沿偏振化方向的分量通过,所以从检偏器透出的光的振幅 \( A_{1}=A_{0}cos\alpha \) 。 由于探测器检测到的是光强,而由光的波粒二象性可知,光强与振幅的平方成正比(I∝A2),因此透过检偏器的光强I2与原光强I1及偏振器角度α之间的关系可以表示为 : \( I_{2}=I_{1}cos^{2}\alpha \) 。
马吕斯定律的应用
马吕斯定律在多个领域有着广泛的应用:
偏光太阳镜: 马吕斯定律应用于制造偏光太阳镜,这种太阳镜可以减少来自水平表面的眩光,比如水面或雪地反射的光线,提高视觉清晰度。 通过调整偏振片的角度,可以控制透过的光强,减少眩光。
摄影中的偏振滤光片: 在摄影中,偏振滤光片被用来减少或消除反光,增强天空和云彩的对比度和饱和度。 通过旋转偏振滤光片,可以改变透过的光强,从而控制照片中的反光和对比度。

液晶显示技术(LCD): LCD屏幕的工作原理涉及到控制通过屏幕的光强度,这正是基于马吕斯定律的应用,通过改变液晶分子的排列来控制光的透过率。