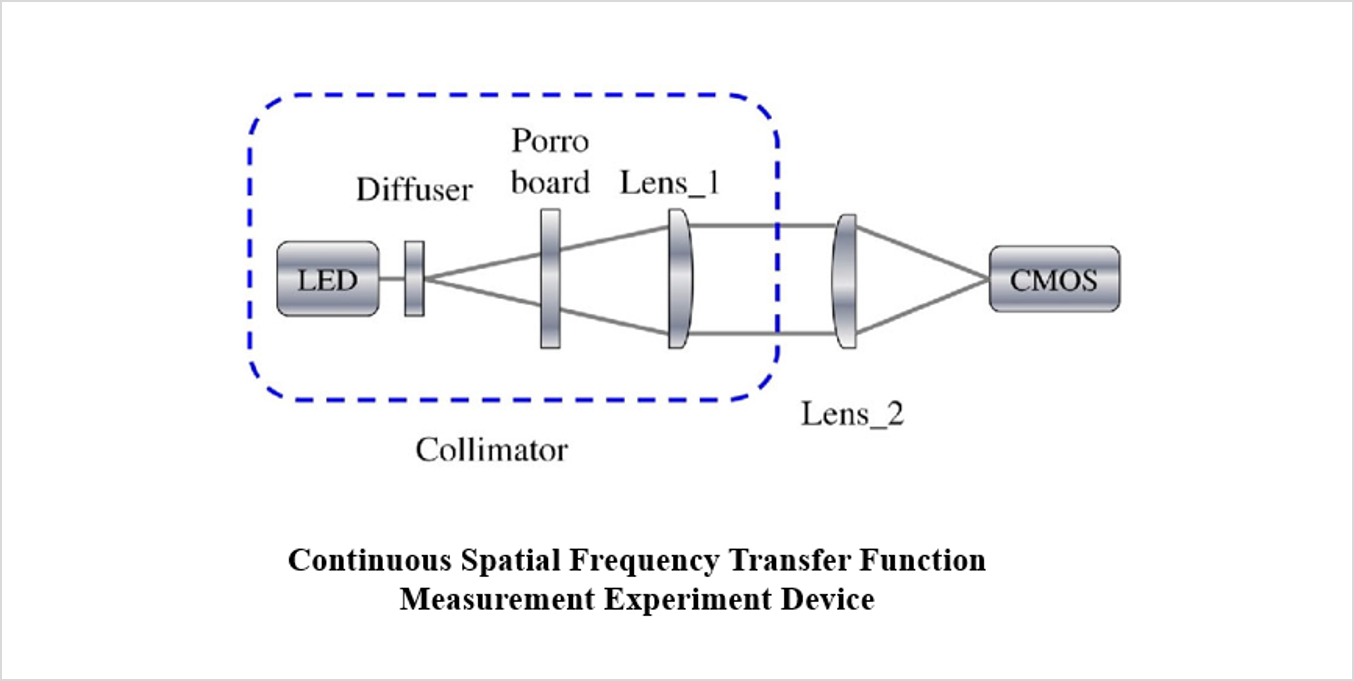
研究光学系统的成像过程和成像质量评价,是现代光学信息处理领域的重要内容。对于光学系统而言,由于系统对光束的限制,它对点物所成的像是一个由系统孔径决定的衍射斑。光学系统对扩展物体所成的像,则是对应于构成物体所有点的衍射斑的叠加。正是由于光学系统的衍射效应,使理想光学系统所成的像不能完全与物体本身相似。光学传递函数可以定量地描述物体频谱中各个频率成分经过光学系统的传播情况,因而它可以从本质上反应物像之间的变化,比较科学地对成像质量作出评价。现在这一理论已经普遍地应用于光学设计结果的评价、光学镜头质量的检测、光学系统总体设计以及光学信息处理等方面。
|
序号 |
型号 |
描述 |
数量 |
|
1 |
PLP-300 |
平行光管,带玻罗板 |
1 |
|
2 |
DR50-450 |
燕尾槽导轨,长度 450.0 mm |
1 |
|
3 |
CB-2-P5 |
压块,固定燕尾槽导轨,最大夹持厚度 3.7 mm,适用于DR50系列导轨,一包五个 |
1 |
|
4 |
HM-V50 |
V型夹持器,夹持直径10 mm~50 mm |
2 |
|
5 |
MV-USB500M |
CMOS相机、2592*1944,单像素尺寸2.2 um |
1 |
|
6 |
SM1-CC |
螺纹转接件,SM1外螺纹和C外螺纹 |
1 |
|
7 |
PH-75A |
Ø12.7 mm连体式接杆支架,夹持直径12.7 mm接杆,叉块可360°旋转,底部磁性底座,H=75 mm |
4 |
|
8 |
OP-75 |
不锈钢接杆,直径 12.7 mm,顶部M4 x 12螺柱,底部M6螺纹孔,L=75 mm |
4 |
|
9 |
DR50F-25 |
燕尾槽导轨滑块,载体平台尺寸 25 mm x 25.4 mm,附带1个M6螺丝 |
4 |
|
10 |
FLF1A |
固定式透镜安装架,SM1内螺纹,适用安装直径Ø25.4 mm光学元件,附带1个SM1R卡环 |
2 |
|
11 |
MCX10615-A |
平凸透镜,N-BK7,增透膜 400 nm-700 nm,直径 25.4 mm,焦距 150.0 mm,安装于SM1标准透镜套筒中 |
1 |
|
12 |
CA-1E |
压臂夹持高度,拓展接杆,长度 31.5 mm,延长V型夹持器的压臂 |
2 |
连续空间频率传递函数测量系统
光学传递函数(Optical Transfer Function, OTF)表征光学系统对不同空间频率的目标的传递性能,能客观有效地分析整套光学系统的信息传递性能,因而广泛应用于光学设计和光学检验。该方法将物体看作由各种频率的谱组成,即把物体的光场分布函数展开成傅里叶级数(物函数为周期函数)或者傅里叶积分(物函数为非周期函数),假设物体是由大量的点光源的连续分布构成,该物体的像为所有点光源像的叠加。由于照明光为非相干光,从各个点光源辐射的光波彼此是不相干的,输出的像是输入平面上各个点的像的强度叠加,因此输出的复振幅分布无法计算得到。在频域中,物体经过非相干光学系统成像后,可以得到物和像的强度分布频谱,比较可得非相干成像的传递函数。
实验原理:
傅里叶光学证明了光学成像过程可以近似作为线性空间中的不变系统来处理,从而可以在频域中讨论光学系统的响应特性。任何二维物体\( \psi _o \left( {\nu _x ,\nu _y } \right) \) 都可以分解成一系列x方向和y方向的不同空间频率 \( \left( {\nu _x ,\nu _y } \right) \) 简谐函数(物理上表示正弦光栅)的线性叠加:
\( \psi _{\rm O} \left( {\xi ,\psi } \right) = \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\psi _o \left( {\nu _\xi ,\nu _\psi } \right)\varepsilon \xi \pi \left[ {\iota 2\pi \left( {\nu _\xi \xi + \nu _\psi \psi } \right)} \right]} } \delta \nu _\xi \delta \nu _\psi \)
式中\( \psi _o \left( {\nu _x ,\nu _y } \right) \) 为\( \psi _o(x,y) \) 的傅里叶谱,它正是物体所包含的空间频率\( \left( {\nu _x ,\nu _y } \right) \) 的成分含量,其中低频成分表示缓慢变化的背景和大的物体轮廓,高频成分则表征物体的细节。
当该物体经过光学系统后,各个不同频率的正弦信号发生两个变化:首先是调制度(或对比度)下降,其次是相位发生变化,这一综合过程可表为:
\( \psi _i \left( {x,y} \right) = H\left( {\nu _x ,\nu _y } \right) \times \psi _o \left( {\nu _x ,\nu _y } \right) \)
式中\( \psi _o \left( {\nu _x ,\nu _y } \right) \) 表示像的傅里叶谱。\( H\left( {\nu _x ,\nu _y } \right) \) 称为光学传递函数,是一个复函数,它的模为调制度传递函数(Modulation Transfer Function, MTF),相位部分则为相位传递函数(Phase Transfer Function, PTF)。显然,当H=1时,表示像和物完全一致,即所成像包含了物的全部信息,没有失真,光学系统成完善像。
但在实际的光学成像系统中,由于光波在光学系统孔径光阑上的衍射以及像差(包括设计中的余留像差及加工、装调中存在的公差),信息在通过光学系统传递过程中不可避免会出现失真。总体而言,被传递的信息中,空间频率越高的部分,其传递效率 越差。
对像的傅里叶谱\( \psi _o \left( {\nu _x ,\nu _y } \right) \) 再作一次逆变换,就得到像的光强分布:
\( \psi _i \left( {\xi ,\eta } \right) = \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\psi _i \left( {\nu _x ,\nu _y } \right)} } \exp \left[ {i2\pi \left( {\nu _x \xi + \nu _y \eta } \right)} \right]d\nu _x d\nu _y \)
(1)衍射受限的含义
衍射受限是指在理想光学系统的成像过程中,受光学系统的孔径光阑影响,光束会发生衍射效应,从而使得在像面上实际得到的是一个具有一定大小的光斑(弥散斑),而不是一理想像点(即点物不成点像)。即便是在理想光学系统中,当超过一定空间频率后,其光学传递函数也等于零。该空间频率称为系统的截止频率,公式如下:
\( \nu _l = 2n'\sin U'_{\max } /{\lambda } \)
式中νl为像方截止频率,n′为像方折射率,U′为像方孔径角,λ为光的波长。据上述,物面上超过截止频率的空间频率是不能被光学系统传递到像面上的。因此,可以把光学系统看作是一个只能通过较低空间频率的低通滤波器。综上,我们通过对低于截止频率的频谱进行分析,就可以对像质进行评价了。在光学术语中,把理想光学系统的传递函数曲线称为该系统传递函数的衍射受限曲线。
由于衍射受限曲线代表系统所能达到的最佳理想指标,而实际光学系统由于存在各种像差,其传递函数值在各个频率上均比衍射受限频谱曲线所对应的值低。
(2)传递函数连续测量的原理
当目标物为一狭缝时,设狭缝的方向为y轴,此时可以认为该狭缝在x轴上是一个非周期的函数(如图 1)。
图 1 目标物狭缝
非周期函数通过傅里叶变换可以分解成无限多个频率间隔的振幅频谱函数。由于该频谱函数是空间频率的连续函数,因此通过对它的传递函数的研究可以得到所测光学系统在一段连续空间频率上的传递函数分布。其中目标物的几何线(即宽度为无限细的线)成像后均被模糊展宽,该展宽线的截面强度分布即为L(x)线扩散函数(line spreading function, LSF),狭缝函数(即从狭缝输出的光强分布的几何像)为\( \eta (x) \) 。根据傅里叶光学的原理,在像面上的光强分布为:
\( L'\left( x \right) = L\left( x \right) * \eta \left( x \right) \)
如果使用面阵探测器,则沿y方向的积分给出L′(x)。上式表明测出的一维光强分布函数为线扩散函数与狭缝函数的卷积。对上式进行傅里叶变换,得到
\( M'\left( \nu \right) = FT\left\{ {L'\left( x \right)} \right\} = FT\left\{ {L\left( x \right)} \right\} \times FT\left\{ {\eta \left( x \right)} \right\} = M\left( \nu \right) \times \tilde \eta \left( \nu \right) \)
式中FT表示傅里叶变换,M(ν)为线扩散函数L(x)的傅里叶变换,即一维光学传递函数,η(v)为狭缝函数的傅里叶变换。上式表明,L′(x)的傅里叶变换为光学传递函数与狭缝函数的几何像的傅里叶变换的乘积。如果已知\( \eta (x) \) ,通过对上式的修正即可得到光学传递函数。
当狭缝足够细,例如比光学系统的线扩散函数的特征宽度小一个数量级以上,\( \eta (x)\approx \delta (x) \) ,就有
\( L'\left( x \right) \approx L\left( x \right) \)
\( M'\left( x \right) \approx M\left( \nu \right) = FT\left\{ {L'\left( x \right)} \right\} \)
对L′(x)直接进行快速傅里叶变换处理就得到一维光学传递函数。
评价光学系统成像质量(像质评价)时通常要对一对正交方向的传递函数进行测量。
参考文献:
[1]王艳、袁素真、罗元.《光电信息专业实验教程》.2020.5

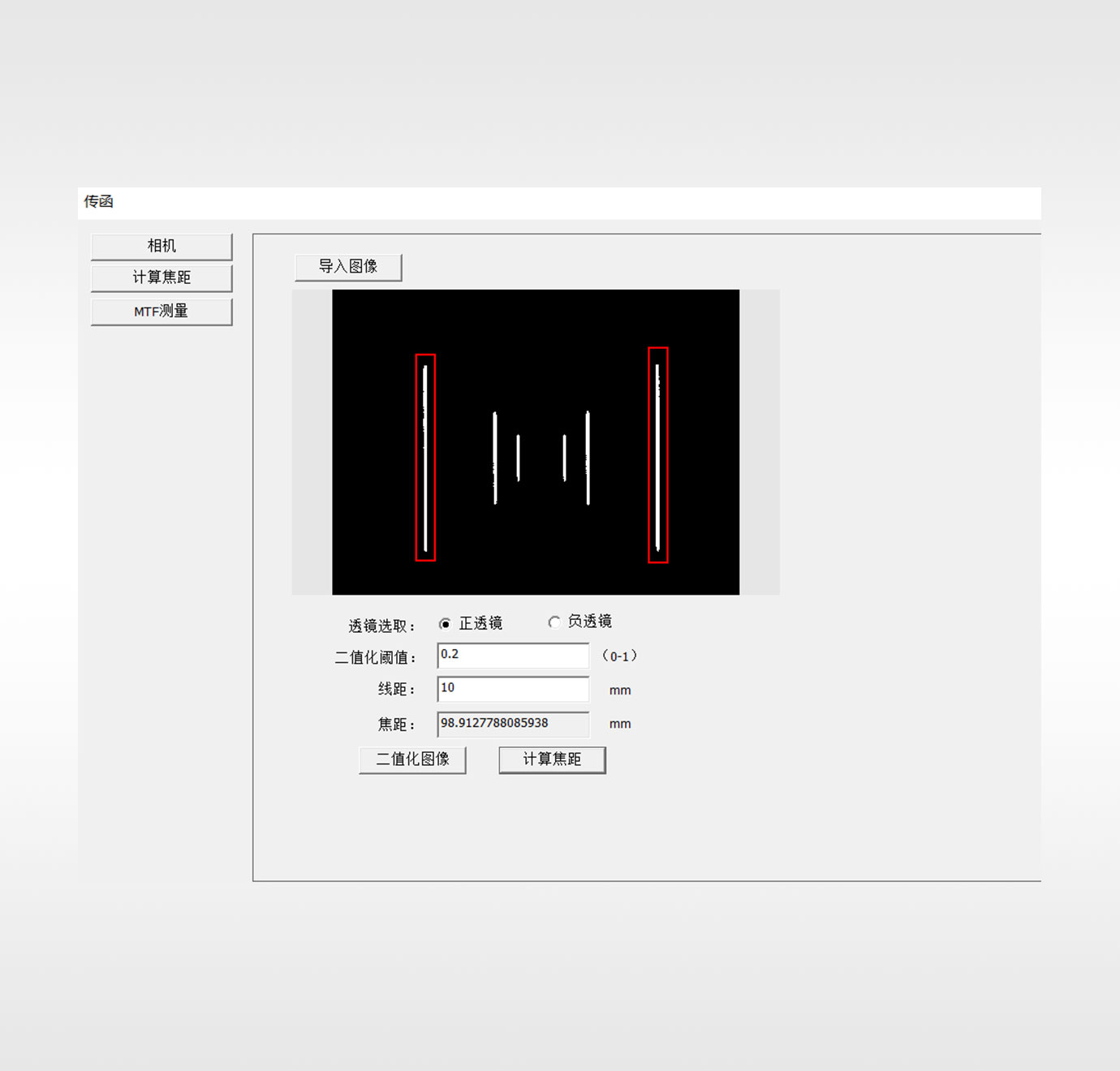
连续空间频率传递函数测量系统是待测镜头对直狭缝(可以看作是一维函数)成像,通过相机进行探测,数据被计算机接收并进行快速傅里叶变换,得到狭缝光强的线扩散函数(LSF),将LSF转换成连续空间频率下的谱函数曲线,即调制传递函数(MTF)。
| 产品型号 |
描述
|
单价 | 对比 | 发货日期 | |||
|---|---|---|---|---|---|---|---|
|
|
CSFTF-BL | 连续空间频率传递函数测量实验装置 | ¥11120 | 6周 |
|
加入购物车 |
| 产品型号 | 波长 | 当前波长(nm) | 当前透射率(%) |
|---|