1609年伽利略通过延续荷兰商人的发现，发明了第一台折射式望远镜，极大推进了人类观察太空的进程。随后，开普勒又在其基础上发明了另外一种望远镜—开普勒式望远镜。受限于当时的加工水平，大口径的折射式望远镜很难实现，并且折射式望远镜非常的笨重，在观察时有色差影响，并不是天文望远镜的最佳选择。（折射式望远镜设计实例：【小麓讲堂】快速设计一个扩束/缩束器）

自1668年，牛顿研制出首台反射式望远镜之后，这种没有色差的望远镜很快便替代了传统折射望远镜，牛顿望远镜结构简单，仅由一个抛物面反射镜与一个转向反射镜组成，并且同等口径的情况下，加工难度远小于折射式，但是其简单的结构也使其不能校正离轴产生的像散和慧差，从而限制其应用范围。（【小麓讲堂】牛顿望远镜设计实例）

其实早在1663年，詹姆斯·格雷戈里提出一种方案，那就是使用一面主镜，一面副镜，与牛顿式望远镜不同的是，它们均为凹面镜，副镜置于主镜的焦点之外，并在主镜的中央留有小孔，使光线经主镜和副镜两次反射后从小孔中射出到达目镜。这种设计可以达到消球差与慧差的效果，所以主镜与副镜均采用抛物面设计，从而使望远镜获得较大的视场，受限于当时的加工水平，这种方案并没有实现。但其为后来人提供了一种思路。

1672年，法国科学家卡塞格林提出了另一种反射镜结构，与格雷戈里的十分相似，不过卡塞格林望远镜副镜采用凸面镜设计，通过利用双曲面和抛物面的反射特性，可以将平行于光轴入射的所有光线汇聚在焦点上；凸面的双曲面反射镜有两个焦点，会将所有通过其中一个焦点的光线反射至另一个焦点上。此类望远镜的镜片在设计上会安放在共享一个焦点的位置上，以便光线能在双曲面镜的另一个焦点上成像以便观测，通常外部的目镜也会在这个点上。抛物面的主镜将进入望远镜的平行光线反射并汇聚在焦点上，这个点也是双曲线面镜的一个焦点。然后双曲面镜将这些光线反射至另一个焦点，就可以在此处观察成像。

下面将用设计实例来深入了解卡塞格林望远镜系统。

根据设计需求和结构图，可直接得到如下参数：

在计算之前，需要先明白一个重要参数：相对口径ｑ，为主镜通光孔径与副镜通光孔径的比值，一般取3。 

通过以上计算，可以确定系统初始结构的部分参数，根据经典卡塞格林系统结构我们可知，主镜为抛物面镜，所以圆锥系数为-1，副镜为双曲面镜，其圆锥系数计算如下：

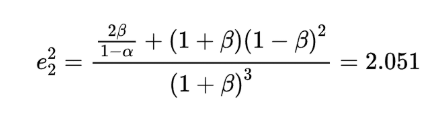
表1给出了不同类型光学元件表面的圆锥系数参数，在一般光学系统设计中常使用k（），查表可得副镜的圆锥系数为-1。

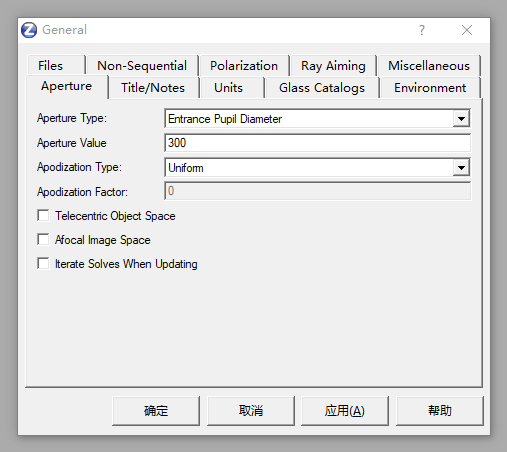
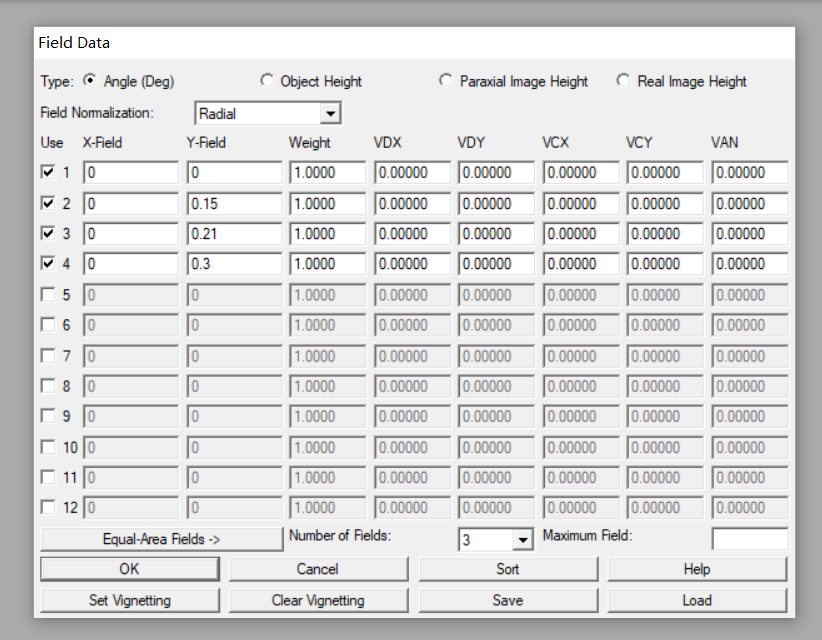
b.设置视场，选择0、0.5和0.7视场(全视场：0.6°)。

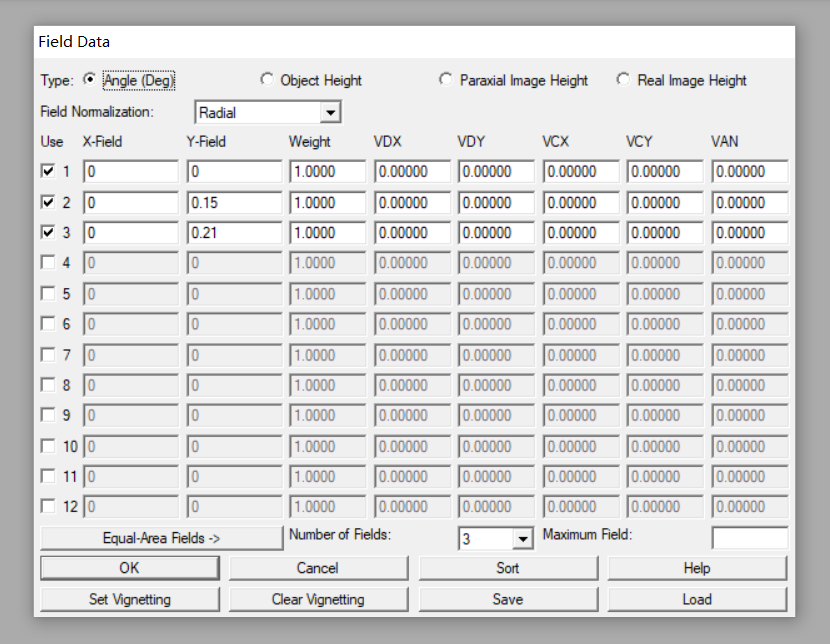
a.首先在STO面材质处输入“MIRROR”，曲率半径处选择F数求解，这时曲率半径会自动计算为4200；也可以直接输入第一步计算“R1”的计算结果。

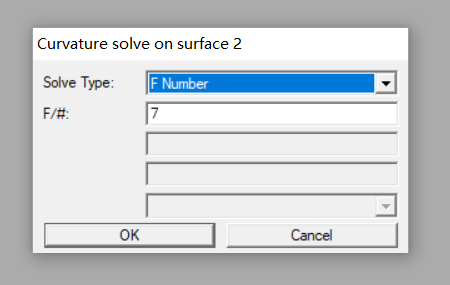
b.在此面厚度栏直接选择边缘光线高度求解，根据抛物面特性，圆锥系数为-1。

c.在STO面前插入一个面，厚度设置为2100 mm，便于观察，此时的系统结构数据如图所示。

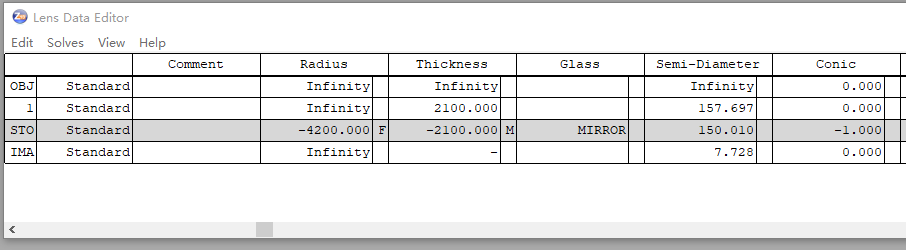
d.观察此时的光线图与点列图，可以看到此时像差以慧差为主，这是反射系统无可避免的。

a.取消STO面厚度处的边缘光线高度求解，设置此面厚度为d，即-1650 mm。

b.在STO面后插入一个面，设置材料为MIRROR，输入计算的“R2”的曲率半径，厚度选择计算方式为边缘光线高度，圆锥系数遵守双曲面规则k<-1（为-e^2）。这里需要注意的是，第一步计算的为一个椭面反射镜，在第一面之后系统局部坐标发生改变，所以输入曲率为计算的负值。

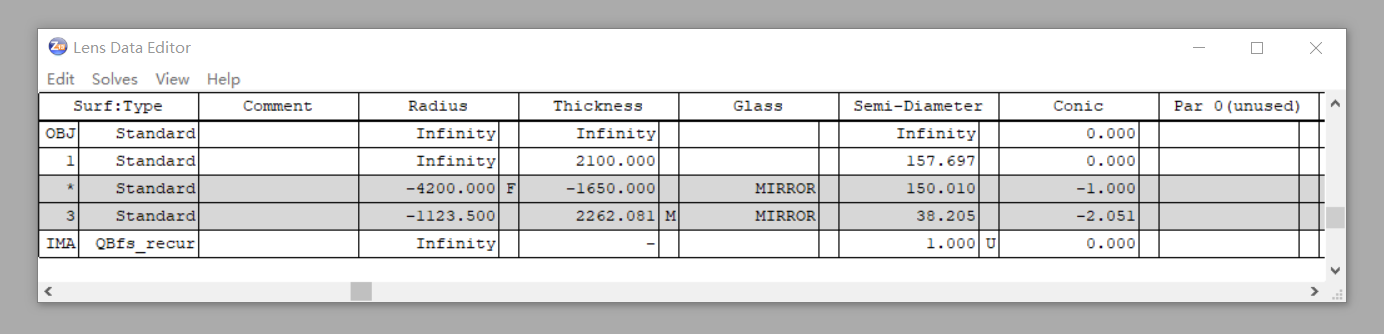
b.双击第2面，将孔径类型改为圆形通光，此时内径尺寸为反射镜遮挡的部分，参考相对口径3：1，设置最小半径为55 mm。

c.查看此时的点列图与MTF曲线。可以看到，此时的光斑基本满足需求，只需要优化遮光孔径提高系统的MTF曲线即可。

a.打开分析菜单栏的光线追迹，并添加边缘视场，查看第三面的光线追迹情况，可以观察到，此面遮光区域约为41 mm。

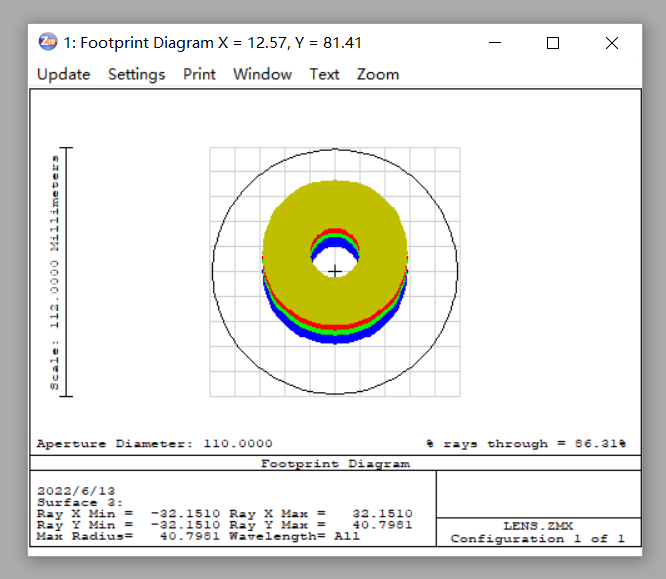
e.更改第二面的遮光区域为41 mm，查看此时的MTF曲线。