一般情况下，自然光在电介质界面上反射和折射时，反射光和折射光都是部分偏振光，只有当入射角为某特定角度时，反射光的偏振态完全是与入射平面垂直的S偏振，折射光的偏振态几乎都是与入射平面平行的P偏振，此时的特定入射角称为布儒斯特角。 光以布儒斯特角入射时，反射光与折射光互相垂直。 利用这一特性，可以产生线偏振光。

通常我们搭建的光路，都会使光束保持相同的高度，入射光和反射光都是和光学平台平行的，因此这里我们可以定义光学平台和入射平面平行，偏振方向竖直的线偏振光为S光，偏振方向水平的线偏振光为P光。 使用线偏振片，我们可以得到任何偏振角度的线偏振光，要得到一束P光或S光，需要将透振轴精确地对准水平或竖直方向，下面介绍一个对准偏振透射轴的常用方法。

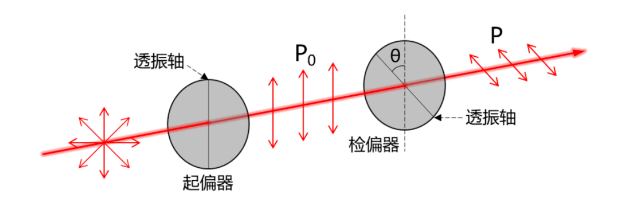
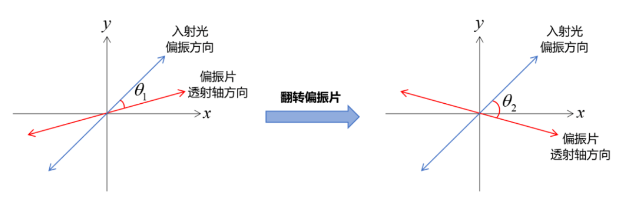
一束功率为P₀的线偏振光入射到偏振片上，假设其偏振方向和偏振片的透振方向夹角为θ₁，则透过偏振片的光功率为\( P_{1}=P_{0}cos^{2}\theta_{1} \) ，翻转偏振片，入射偏振方向和翻转后的透振方向夹角为θ₂，透过偏振片的光功率为\( P_{2}=P_{0}cos^{2}\theta_{2} \) ，当偏振片的透振方向不在水平或竖直方向上时，则\( \theta_{1}\ne \theta_{2} \) ，\( P_{1}\ne P_{2} \) ，因此偏振片翻转前后透过的光功率不相等。

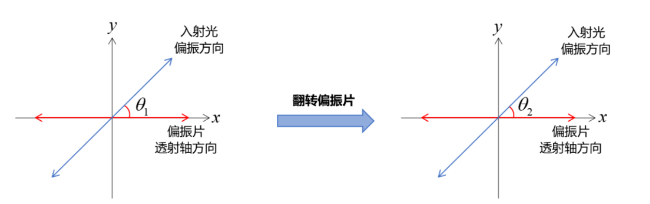
当偏振片的透射轴方向水平或竖直时，入射光从正面入射和背面入射时与透射轴的夹角相等，即 \( \theta_{1}=\theta_{2} \) ，\( P_{1}=P_{2} \)  ，偏振片翻转前后透过的光功率相等。

以生成一束P光为例，我们需要将偏振片的偏振透射轴对准至水平位置，为了精确地调整偏振片的角度，可以使用带有微分头的旋转调整架进行调节。

带有微分头的旋转调整架

首先，使用偏振片LP₀对入射光进行起偏，旋转其偏振透射轴至水平和竖直之间的角度，将偏振片LP₁放在偏振片LP₀后并大致旋转其透振轴至水平角度，使用功率计测量透过偏振片LP₁的光功率记为I，翻转偏振片LP₁后再次测量透过的光功率记为I'，此时\( I\ne I' \) ，说明偏振片LP₁的透振轴角度不水平。 计算翻转偏振片LP₁前后透过光功率的平均值为(I+I')/2，使用微分头再次调整偏振片LP₁的角度，使透过的光功率等于平均值后，再次翻转偏振片LP₁，看翻转前后测得的光功率是否相等，如不相等则继续微调，直至偏振片LP₁翻转前后透过的光功率相等时，偏振片LP₁的透振轴即对准水平方向，此时可以撤去偏振片LP₀，透过偏振片LP₁的为P光。

要得到一束竖直偏振光，即S光，我们可以用相同的方法，只需要将偏振片LP₁更换为偏振片LP₂，并将其透振轴角度大致调至竖直，然后将其翻转前后的透射光功率微调至相等即可。

我们也可以直接利用调至水平角度的偏振片LP₁，将偏振片LP₂放至偏振片LP₁后面，调整偏振片LP₂的透振轴角度，并使用功率计测量其透射光的功率，直至测得的光功率达到最小值，撤去偏振片LP₁，我们便得到一束竖直偏振光，即S光。

借助水平和竖直方向的偏振片，我们还可以得到一束 和水平方向成 45 °的线偏振光 ，如下图，取一片偏振片LP₃ 放至已调至水平和竖直方向的偏振片LP₁ 和偏振片LP₂ 之间，其透振轴方向与偏振片LP₁ 和偏振片LP₂ 的透振轴夹角分别为θ₁ 和θ₂ ，设入射光经过偏振片LP₁ 后的能量为I₀ ，经过偏振片LP₃ 后的能量为I₁ ，经过所有偏振片后的能量为I₂ 。

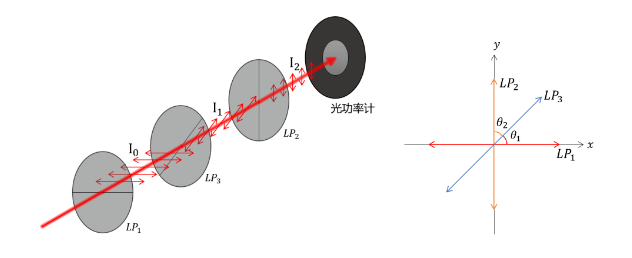
根据马吕斯定律可知：

    \( I_{1}=I_{0}cos^{2}\theta_{1} \)

    \( I_{2}=I_{1}cos^{2}\theta_{2}=\frac{1}{4}I_{0}\left( sin^{2} \theta_{1}\right)^{2} \)

所以，我们只需要旋转偏振片 LP₃ ，使透过所有偏振片的光功率达到最大值，然后撤去偏振片 LP₁ 和偏振片LP₂ ，即可得到一束和水平方向成 45 °的线偏振光。