技术中心

6种测量透镜焦距的常用方法

发布时间：2024-08-29 09:14:48 阅读次数：1974

透镜焦距原理介绍

焦距也称为焦长，是光学系统中衡量光的聚集或发散的度量方式，指平行光入射时从透镜光心到光聚集之焦点的距离。具有短焦距的光学系统比长焦距的光学系统具备更佳的聚集光的能力。简单来说焦距是透镜的主点到焦点之间的距离。

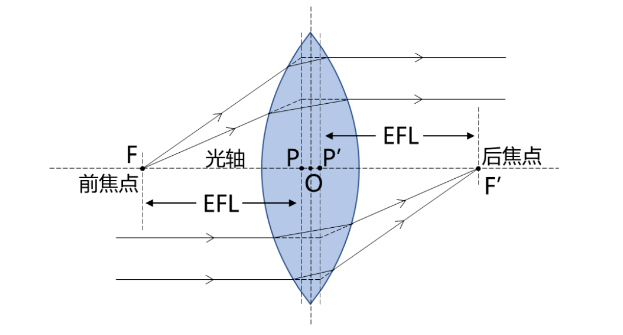
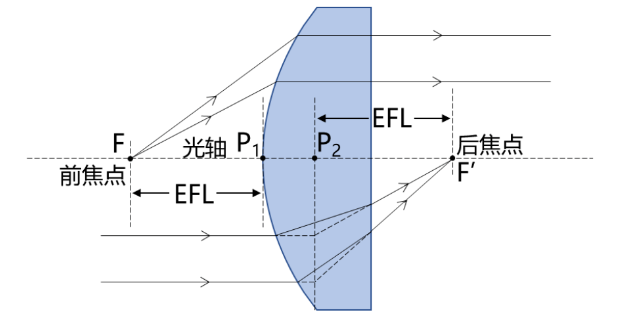
以一片薄的透镜为例，通常认为透镜的中心点（即光心，如图中点O所示）即为主点；那么此时的焦距即为沿着光轴从主点到焦点的距离。而对于具有一定厚度的透镜，我们可以更详细地将主点分为前主点和后主点。从前焦点（物方焦点）发出的入射光线（及其延长线）与平行出射光线（及其延长线）相交，由交点集合所构成的面称为前主面，前主面与透镜光轴的交点就是前主点（或第一主点、物方主点），如图点P所示；相应地，平行入射光线（及其延长线）与聚焦出射光线（及其延长线）相交，由交点集合所构成的面称为后主面，后主面与透镜光轴的交点就是后主点（或第二主点、像方主点），如图点P'所示。此时从主点到焦点的距离即为透镜的有效焦距（EFL），物方焦点与物方主点的距离称为物方焦距；像方焦点与像方主点的距离称为像方焦距。

跟双凸透镜不一样的是，平凸透镜主点落在P₁ 和P₂上， P₁位于凸面顶点。由于另外一个面是平面，所以在知道透镜凸面的曲率半径 R和透镜材料折射率n 的情况下可以根据公式 \( EFL=\frac{1}{\left( n-1 \right)\left( \frac{1}{R_{1}}-\frac{1}{R_{2}} \right)}=\frac{R}{n-1} \) 计算出EFL。

透镜焦距测量方法

当在实验室中遇到那些没有标识的透镜时，为了方便使用，需要对其焦距进行测量，以下将介绍几种测量透镜焦距的常用方法。

自准直法

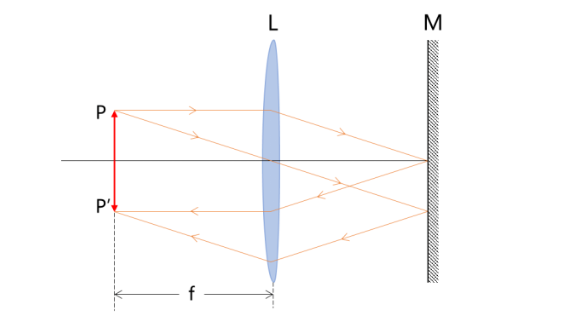
如图所示，P为物体，L为凸透镜，f为凸透镜的焦距，M为平面镜。若物体处于凸透镜的前焦平面上，物体上任一点发出的光束经过凸透镜成为平行光束，平行光由平面镜反射后仍为平行光，再经过凸透镜必然会聚于焦平面上，得到与原来物体等大的倒立实像P'，此时物体与透镜之间的距离就等于透镜的焦距。

二次成像法

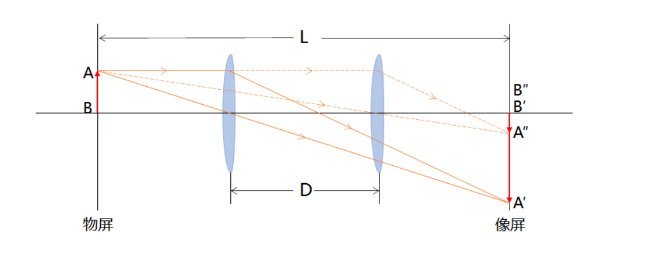
使用二次成像法测量透镜的焦距f，需使物屏与像屏的间距 \( L>4f \) 并固定不变，在物屏和像屏之间移动待测透镜，可以在像屏上得到一个清晰放大的像或一个清晰缩小的像。测量透镜两次成像时位置的距离D，根据公式 \( f=\frac{L^{2}-D^{2}}{4L} \) 即可算出待测透镜的焦距。

平行光管法

平行光管是一种能发射平行光束的精密光学仪器，它有一个质量优良的准直物镜L_o，其焦距是经过精确测定的。在平行光管内物镜的焦平面上有一块表面上刻有多组标准线对的透明玻璃板，称为玻罗板。用小电珠照明玻罗板，玻罗板上每点发出的光束经物镜后转变为平行光束。平行光束经待测透镜后成清晰像于目镜的分划板上，只需测出玻罗板线对的像高，即可算出待测透镜的焦距。原理图如下：

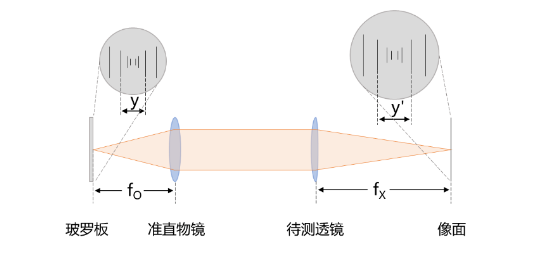
玻罗板某一线对的间距y和平行光管物镜的焦距f_o是已知的，由玻罗板发出的光经平行光管物镜L_o后成为平行光，该光束经待测透镜L_x后成像在其焦平面上，使用测微目镜测出珀罗板像上同一线对的间距y'，则待测透镜焦距f_x可由公式 \( f_{x}=-\frac{y^{'}}{y}\cdot f_{o} \) 求出。

焦度计法

焦度计比较适用于长焦距透镜的焦距测量，其测量原理示意图如下：

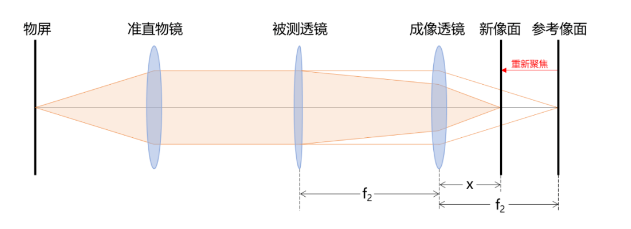
首先，光路中不放入被测透镜，左侧物屏上的观测目标经过准直物镜后变成平行光，平行光束由焦距是f₂的会聚镜会聚，清晰成像在参考像面处。光路校准好后，将被测透镜放入光路中，被测透镜与会聚镜间的距离为f₂，这样一来，由于被测透镜的作用，光束会发生重新聚焦，像面位置发生偏移，会在新像面的位置（参见上图）实现清晰成像，新像面与会聚镜的间隔为x，根据物像关系，可以推理出被测透镜的焦距为： \( \frac{1}{f}=\frac{1}{f_{2}}-\frac{x}{f_{2}^{2}} \)

莫尔偏折法

基于几何光学原理测量焦距的方法在测量过程中易受读数等视差的影响，且在长焦距的测量中常常受到测长仪器和轨道的限制难以实现高精度测量。为了解决这类问题，学者们提出了很多基于Talbot-Moiré技术的测量方法，并且通过Talbot-Moiré条纹变化信息实现了长焦距的测量。

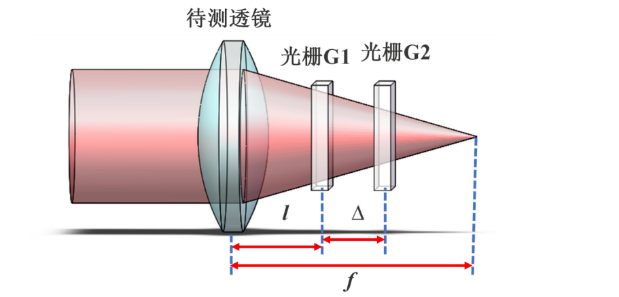
莫尔偏折法的测量结构如图所示，将两个周期均为p的朗奇光栅G1和G2置于待测透镜后方的l处，并且G1和G2间确保一个∆的距离，光栅周期p在经过∆后的周期变为p′，其两者间的关系满足以下公式：\( p^{'}=\frac{f-l-\Delta}{f-l}\cdot p \)

当通过G1的条纹通过第二个朗奇光栅将会叠加成莫尔条纹，其莫尔条纹的周期数与待测透镜焦距f的关系为：\( f=\frac{\alpha\cdot\Delta}{p\cdot N} \) ，式中α为待测透镜的通光孔径，N为莫尔条纹的数目。通过计数莫尔条纹的数目N，结合光栅周期p、间距∆和孔径α的大小，根据公式即可计算出待测透镜的焦距f，但其测量精度受限于莫尔条纹的计数精度。

准直Talbot-Moiré法

为了解决条纹计数误差问题对测量精度的影响，可通过判别莫尔条纹的角度变化信息来实现焦距的测量。如图所示，激光器发出的光束通过透镜和空间滤波器后形成点光源，准直镜将点光源准直为平行光束，当平行光束经过两块周期相等，夹角为θ₁和θ₂的光栅G1和光栅G2，在第二个光栅后放置的相机上采集莫尔条纹。

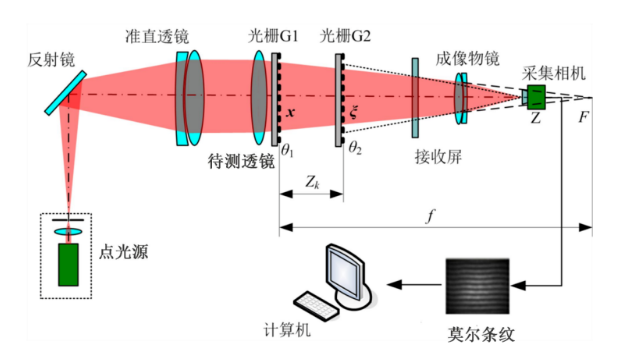
将待测透镜置于光栅G1前的准直光束中，沿着轴向方向缓慢移动光栅G2，直至相机中能采集到清晰的莫尔条纹时，记录光栅G1和G2的距离为Z_k，利用相机采集莫尔条纹，通过图像处理技术获得条纹角度α_k，测距仪标定移动距离Z_k，即可根据公式： \( f=\frac{Z_{k}}{sin\left( \theta_{1}-\theta_{2} \right)tan\alpha_{k}+cos\left( \theta_{1}-\theta_{2} \right)-1} \) ，计算出待测透镜的焦距f。

其中移动的距离Z_k应满足： \( Z_{k}=\frac{kp^{2}}{\lambda} \) ，k=1,2,3...

参考文献

[1]李晓磊.基于平行光管法的薄凸透镜焦距测量[J].应用光学,2019,40(05):859-862.

[2]龚渭.球面光学元件的曲率半径和焦距测量方法研究[D].江苏科技大学,2023.

[3]饶世贤,刘仁明.一种简单测量凸透镜焦距的方法[J].大众科技,2011,(01):24-25.

[4]杨春宝,尤政,王伯雄.莫尔偏折法测透镜焦距中的条纹二值化方法[J].光学技术,2004,(02):206-208.

{{item.product_sn}}

{{item.category_name}}