揭秘光学薄膜之截止滤光膜&带通滤光膜
发布时间:2024-07-08 17:54:36
阅读次数:2835
光学薄膜是在光学元件或独立基板上,制镀单层或多层介电质膜、金属膜,和这两类膜的组合膜,以改变光经过元件时的传递特性,包括光的透射率、反射率、吸收率、散射、光场局部的偏振及相位等。光学元件表面附着的薄膜厚度薄而均匀,且种类繁多。 下面主要介绍截止滤光膜和带通滤光膜的作用和选型要点。
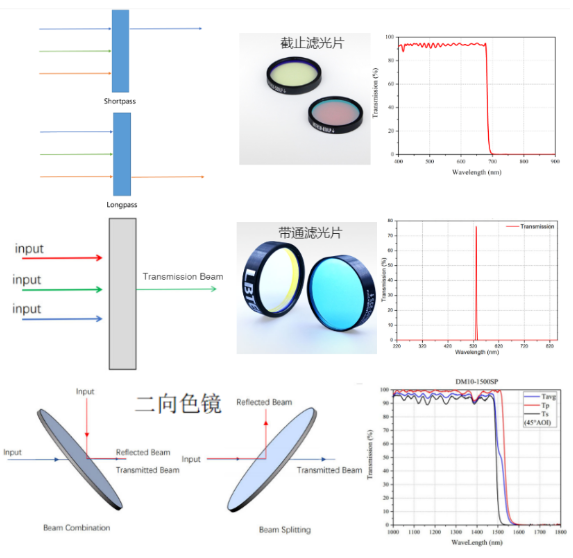
截止滤光膜要求在某一波段范围内的光束高透射,而偏离这一波段的光束骤然变化为高反射(抑制)。 通常把需垂直入射条件下,抑制短波区、透射长波区的滤光片称为长波通滤光片; 而将抑制长波区、透射短波区的滤光片称为短波通滤光片。 下图为长波通滤光膜和短波通滤光膜的典型特性曲线。
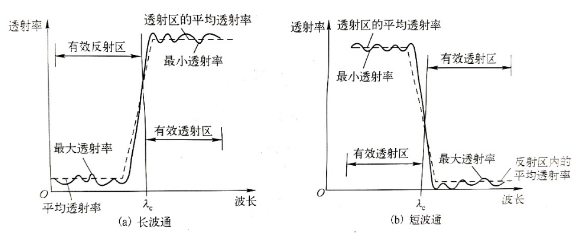
1.截止/起始波长: 是指 透射曲线开始下降(上升)时的波长;
2.通带/通带透过率: 对应为高透射带的光谱宽度、平均透过率;
3.截止带/截止带光密度: 低透过带的光谱宽度及平均OD值,其中\( OD\left( \lambda\right)=-log\left(T\right) \) ,OD值越大,阻带/截止带的透过率越低,滤光的效果就越好。
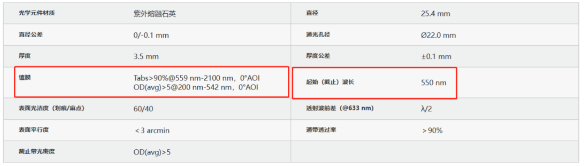
这些重要参数也能更快的指引选型。 例如,常见的荧光检测中,当探测器同时接收到测量面的激发光532nm和发射光580nm两个波长的光时,可在相机前增加一片550nm的长波通滤光片MEFH10-550LP,来实现相机只接受发射光有效信号,消去激发光的干扰。
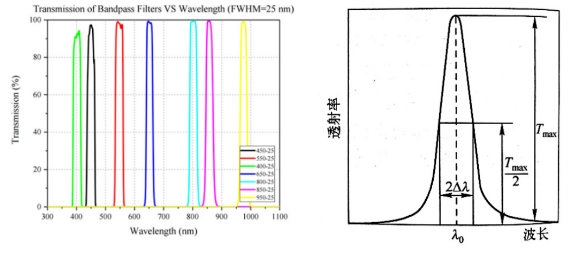
带通滤光膜是指在一定的波段内,只有中间一小段是高透射率的通带,而在带通两侧是高反射率的截止带。
1. \( \lambda_{0}: \) 带通滤光膜的中心波长;
2. \( T_{max}: \) 中心波长的透射率,也称峰值透射率;
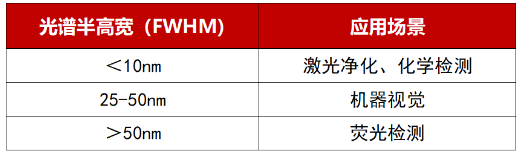
3 . 光谱半高宽(FWHM): 峰值透射率一半对应的波长宽度,即带通宽度;
4. 阻带: 两侧低透过带,其中\( OD\left( \lambda\right)=-log\left(T\right) \) ,OD值越大,阻带/截止带的透过率越低,截止的效果就越好。
通常来说,带通滤光膜有两种结构形式: 一种是长波通滤光膜系+短波通滤光膜系的重叠通带波段形成的带通滤光膜的通带。 这种结构的光谱特性可以获得较宽的截止带和较深的截止度,但不容易获得很窄的通带,所以常用于宽带通滤光膜。 第二种是法布里-珀罗干涉仪形成的滤光膜系,这种结构的光谱特性可以获得窄带,但截止带不深。 所以大多数情况下要配合截止带滤光膜来拓宽截止带和增加截止深度。
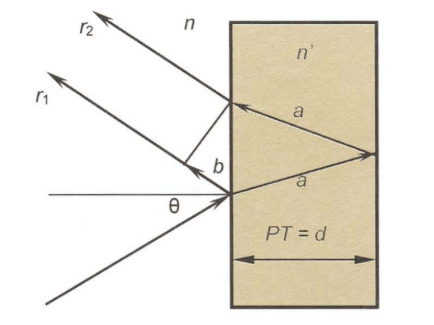
金属-介质法布里-珀罗滤光片(右图)
F-P干涉仪由两个反射率分别为\( R_{1}、R_{2} \) ,间隔为d的反射板组成。 当此结构换成两个金属反射层夹一个介质层的薄膜组合结构时,该类型的滤光膜即被称为金属-介质法布里-珀罗滤光膜,其透射率为\( T=\frac{T_{0}}{1+F\cdot sin\left(\theta \right)^{2}} \) ,其中\( T_{0}=\frac{T_{1}\cdot T_{2}}{(1-\sqrt{R_{1}\cdot R_{2})}^{2}} \) ,\( F=\frac{4\sqrt{R_{1}\cdot R_{2}}}{(1-\sqrt{R_{1}\cdot R_{2})}^{2}} \) ,\( \theta=\frac{\varphi_{1}+\varphi_{2}}{2}-\frac{(2\pi nd)}{\lambda} \) 。 式中 \( R_{1}、R_{2}、T_{1}、T_{2} \) 分别为两反射膜的反射率和透过率;\( \varphi_{1}、\varphi_{2} \) 为反射膜的反射相移,λ为波长,n为薄膜折射率,d为薄膜间隔层间距。 提高反射膜的反射率可以压缩带宽,但是对于金属-介质法布里-珀罗滤光膜而言,过于减小带宽会导致峰值透过率显著下降 。 金属膜的吸收较大,如果改用多层介质反射膜代替金属反射膜,可大大提高滤光片的性能。
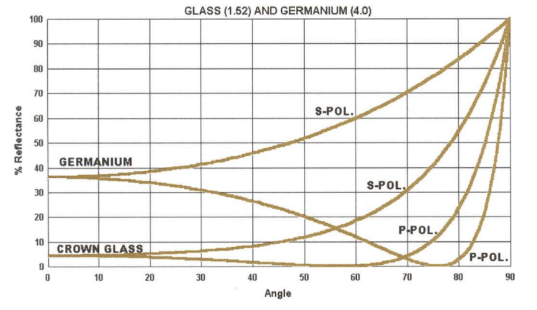
当光束垂直入射到滤光片时,电矢量垂直于入射面的振动分量(S分量)和平行于入射面的振动分量(P分量),对于薄膜层来说折射率是相同的。 而当光束斜入射到滤光片时,这两种分量对于薄膜界面的情况就不同了,S分量的有效折射率为 \( n_{s}=ncos\left( \theta \right) \) ,P分量的有效折射率为\( n_{p}=\frac{n}{cos\left( \theta \right)} \) ,其中n 是膜层折射率, θ是膜层中的入射角; 反射系数为\( r_{s}=\frac{(n_{1s}-n_{2s})}{(n_{1s}+n_{2s})} \) ,\( r_{p}=\frac{(n_{1p}-n_{2p})}{(n_{1p}+n_{2p})} \) ,此时s光和p光的反射率在不同的入射角下均有较大的差别,下图以1.52折射率玻璃和4.0锗片为例。
如果膜层的物理厚度为d ,并且光以θ为入射角入射,此时在光从膜层第一面入射再到从第二面膜层返回到第一面的路径为2a,且2a大于2d,斜入射会导致光在膜层中的实际光程2an’大于了垂直入射的光程2dn’。 在整体看待r1和r2光束时,r1 在折射率n的介质中比r2多走的光程为nb,更多的研究表明,\( nb\gg2a-2dn' \) 。 因此斜入射时,经过薄膜两光束的光程差值变小,膜层的光谱向短波方向移动。
综上得知,当倾斜入射到滤光片或改变二向色镜入射角度时,Snell定律和偏振效应就会发生作用,随着角度的增大,膜系的有效波长会向短波方向移动,且截止带边沿陡度和通带带宽均会受到较大影响。
[1]卢进军,刘卫国,潘永强. 光学薄膜技术[M]. 第2版. 电子工业出版社, 2011.
[2]李宇航, 谢宜风, 刘军英. 光学功能薄膜的制造与应用[M]. 第一版. 化学工业出版社, 2012.
[3]范正修. 光学薄膜及其进展[J]. 光学学报, 2011, 第31卷(9).
[4] Willey R R .Field Guide to Optical Thin Films[M]. 2006.