技术中心

利用全息电介质超表面实现偏振切换光场涡旋线的打结

发布时间：2020-04-22 10:22:04 阅读次数：1222

导读

构造新型多自由度结构光场是光场调控领域的研究热点之一。其中，光场中的拓扑结构，如与相位奇异性相关的涡旋结和链，在基础研究和实际应用中引起研究者们极大的关注。近日，西北工业大学的赵建林研究团队提出并通过实验证明了一种电介质的全息超表面器件，可以在微纳尺度上构造光学涡旋结和链。该器件可以通过改变入射光的偏振来切换两种不同的拓扑结构。此外，利用数字全息干涉法，准确地表征了涡旋线的三维拓扑结构，并展示了这种超小场的拓扑保持演化特性。该工作有望促进结构光场在微纳尺度上的应用，以及其他超小尺寸物理场的构建。相关成果以“Tying Polarization‐Switchable Optical Vortex Knots and Links via Holographic All‐Dielectric Metasurfaces”发表在期刊Laser & Photonics Reviews 上。该论文第一作者为西北工业大学郭旭岳博士，通讯作者为赵建林教授和李鹏副教授。

作者简介

郭旭岳，西北工业大学，理学院博士生，研究方向为光学超表面。所在团队为西北工业大学理学院赵建林教授带领的微纳光子学与信息光学研究团队，该团队主要研究方向包括：数字全息术及应用、微纳光子学与光子器件、新型光场产生与调控技术、光纤技术及应用。

研究背景

自1992年Allen指出拉盖尔-高斯光束中与方位角相关的螺旋相位具有轨道角动量(Orbital Angular Momentum, OAM)后，包含相位奇点的光场已经被广泛地研究和应用于各种领域。近年来，一种在有限空间内具有打结涡旋线(三维空间中相位奇点的演化轨迹)的特殊光场引起了人们的极大关注。该现象最早由Lord Kelvin在19世纪后期提出，理论认为原子是在无粘性流体中打结的漩涡，随后该理论在流体动力学、量子场论、等离子体等领域体现出了重要作用。光学领域中，光场中的结链结构理论最初由Berry和Dennis于2001年提出，随后由Leach等人通过线性叠加拉盖尔-高斯光束实现了实验上的产生。

具有打结涡旋线的特殊光场可以作为量子力学物质波的拓扑波导，如玻色-爱因斯坦凝聚。精确再现结链光场的振幅与相位，利用空间光调制器(Spatial Light Modulator, SLM)通过全息的方式产生是最简单有效的方法。然而在实际实现过程中，结链结构对调制的高斯分布宽度较为敏感，其纵向尺度随横向尺寸的增大而增大，并且由SLM带来的体积大、系统复杂度高以及无法多参量调控等缺点严重阻碍了其在微纳光学和纳米光子集成等领域的进一步研究与应用。

研究内容

针对上述问题，本文提出了一种基于几何相位与传输相位联合调控的全息电介质超表面，实现了两种具有超小尺寸拓扑结构光场的多通道产生。图1(a)给出了通过全息介电质超表面实现光学涡旋结与链的示意图，该超表面由几何尺寸和取向角不同的硅纳米柱组成。通过将几何相位与传输相位相结合，当偏振态为\( |\Psi _{0}\rangle \) 的光入射时，该超表面将会产生两个携带不同的相位调制信息(\( \varphi ^{+} \) 和\( \varphi ^{-} \) )的正交偏振态，\( |\Psi^{+}\rangle \) 和\( |\Psi^{-}\rangle \) 。在此相位信息的调制作用下，光束将在三维空间中形成光学涡旋结和链，并且通过改变入射光的偏振态可以进行涡旋结与链的切换。

根据上述原理，首先通过拉盖尔-高斯光束的线性叠加来计算孤立涡旋结链的复振幅分布。在束腰平面，其可表示为\( \psi _{link,knot}=\sum a_{i}LG^{l}_{p}\left ( \omega \right) \) ，其中\( LG^{l}_{p}\left ( \right) \) 表示拉盖尔-高斯光束，\( l \) 、\( p \) 分别为角向与径向指数，\( a_{i} \) 为叠加系数，\( \omega \) 为束腰宽度。这里我们选取经典的Trefoil knot和Hopf link作为拓扑结构，其在束腰平面(z = 0平面)的复振幅分布如图1(b)(c)所示。实验中，由于超表面一般只对相位参数有调制作用，所以这里使用反sinc函数纯相位编码技术，将振幅信息作为掩模编码到相位函数上生成纯相位全息图，并附加了倾斜相位将各空间频谱分开。

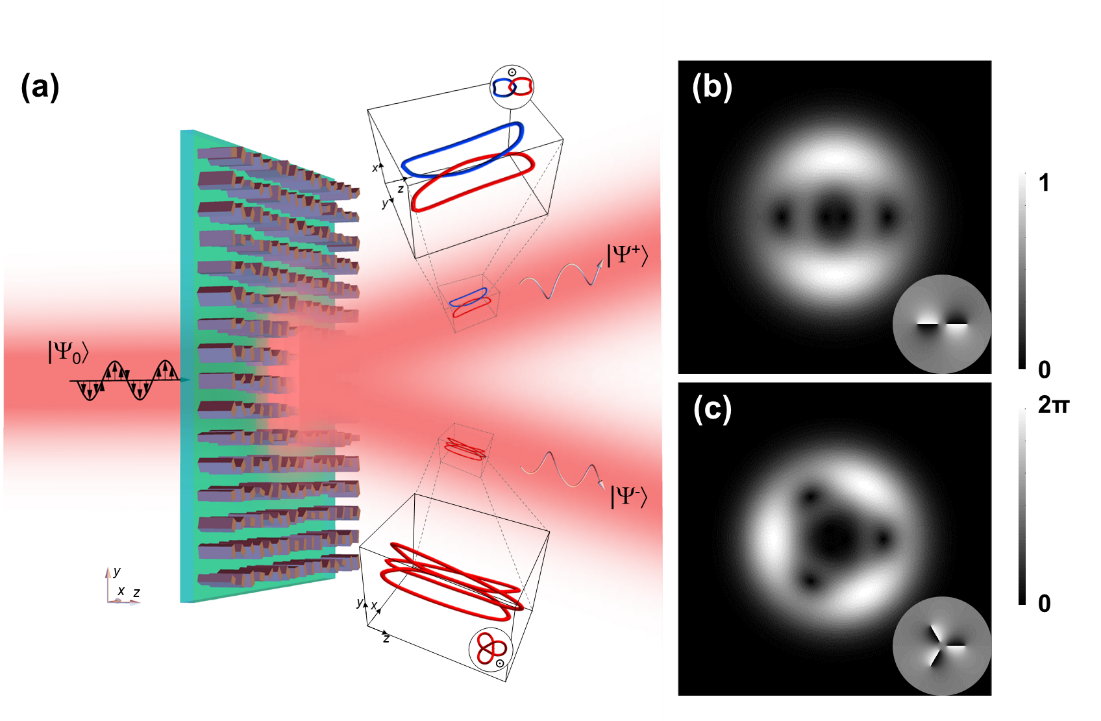
图1.(a) 利用全息介电质超表面实现拓扑结构光场多通道产生的原理示意图。超表面由具有不同几何尺寸和取向角的纳米柱周期性排列组成，可在不同的偏振态(\( |\Psi^{+}\rangle \) 、\( |\Psi^{-}\rangle \) )上施加不同的相位调制。插图：光学涡旋结(Trefoil knot)与链(Hopf link)的三维结构示意图。(b)、(c) Hopf link和Trefoil knot在光束束腰(z = 0)平面上的振幅和相位分布。

在超表面设计过程中，选取左旋与右旋圆偏振光来实现这种相位分布，并以此将目标相位信息(\( \varphi ^{+} \) 和\( \varphi ^{-} \) )转换为纳米结构的选取参数，即\( \varphi_{x} \) 、\( \varphi_{y} \) 以及方位角\( \theta \) 。经理论计算，各参数具有如下关系\( \varphi_{x} =\left ( \varphi^{+} + \varphi^{-} \right )/2 \) ，\( \varphi_{y} =\left ( \varphi^{+} + \varphi^{-} \right )/2-\pi \) ，\( \theta= \left ( \varphi^{-} + \varphi^{+} \right )/4 \) 。超表面的结构选取为熔融石英基片和沉积多晶硅组成的双层材料，石英基底厚度为500 μm，多晶硅材料为615 nm，结构周期为450 nm。通过时域有限差分法对结构的参数进行了二维扫描，得到透射振幅和相位随硅纳米柱长度和宽度的函数。进一步利用上述结构参数之间的关系选取了17种结构，并通过电子束曝光和等离子刻蚀等技术制备了该超表面器件，如图2(a)(b)所示。为了能够准确地测量超表面产生的光学涡旋结链，搭建了如图2(c)所示的扫描干涉测量光路。干涉法可以精确地测量到光束的振幅与相位信息，而由三角棱角和位移台组成的回路可以扫描测量其三维结构。

图2. (a)、(b) 超表面的扫描电子显微镜图像和局部图案的放大图像。(c) 测量光场拓扑结构的扫描干涉测量实验装置。

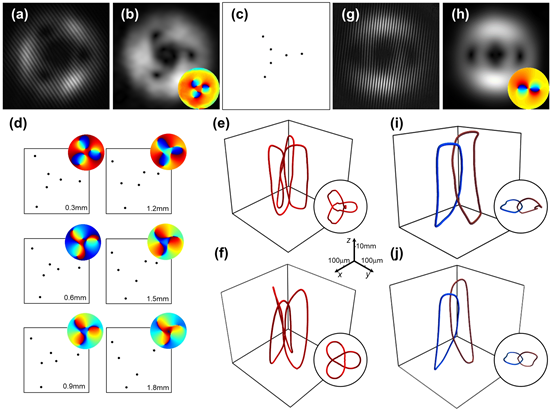
图3(a)给出了在右旋圆偏振光入射条件下，测量到的Trefoil knot场在光束束腰平面处的干涉图，通过数字全息解调，可得到其振幅与相位分布，如图3(b)所示，与图1(c)中的目标场相比，实验结果与理论一致。如何准确地定位相位奇点是测量涡旋拓扑结构的关键，因此，借助局部空间频率将相位奇点从背景中提取出来，相比于传统的过度曝光方法，该方法能够更准确地定位涡旋奇点，尤其是涡旋线在三维空间的拐点。如图3(c)中的六个黑点描绘了用这种方法得到的相位奇点位置。进一步，通过在z方向上以500 μm为间隔扫描了多个平面来测量相位奇点在三维空间中的分布，将其连接起来得到三维结构(图3(e))。图3(d)给出了多个平面上的相位奇点位置和相应的相位分布。可以看出，六个相位奇点的位置随着光束的传播而演化，特别是在z = 1.8 mm平面上，右上角的两个奇点相结合，说明这两个涡旋线在这个平面上形成了一个回路。需要说明的是，在实际实验中，由于波束倾斜或空气扰动等实验误差的影响，其他四个相位奇点未在同一平面上同时结合。另一方面，这种现象恰恰说明了这种定位方法的准确性。经测量，Trefoil knot的直径大约是220 μm，纵向长度大约是36 mm。

图3. (a) Trefoil knot场在光束束腰平面处的干涉图。(b) 通过干涉图解调出的强度与相位分布。(c) 通过特殊算法计算出的奇点位置分布。(d) 不同传播平面处的奇点位置分布及相位分布。(e), (f) 实验测量和数值计算得到的Trefoil knot结构。(g) Hopf link场在光束束腰平面处的干涉图。(h) 通过干涉图解调出的强度与相位分布。(i)、(j) 实验测量和数值计算得到的Hopf link结构。

为了演示光学涡旋结链多通道产生的偏振切换特性，将入射光改变为左旋圆偏振光，并调节\( 4f \) 滤波系统的位置，将在另一侧得到Hopf link，如图3(g)(h)所示的Hopf link场在光束束腰平面处的干涉图和解调出的强度与相位分布。相同地，通过扫描测量，得到了Hopf link场涡旋线的三维结构，如图3(i)所示。同时，给出了理论计算的三维结构作为对比，如图3(f)(j)所示。此外，当入射光具有左旋和右旋圆偏振光的叠加状态时，如线偏振光，该超表面器件将同时产生两种拓扑结构，比值取决于入射光的偏振椭圆度。该超表面的总效率约为54.5%。

研究总结

本文提出了一种基于几何相位与传输相位联合调控的全息电介质超表面，实现了两种具有超小尺寸拓扑结构光场的多通道产生。通过调控入射光的偏振态，如入射光的旋向，可以在可切换的偏振通道中实现光学涡旋结（Trefoil knot）与链（Hopf link）的产生。为精准地测绘涡旋线的拓扑结构，采用基于数字全息术的扫描干涉测量法，并借助局部空间频率将相位奇点从背景中提取出来。相比于传统的过度曝光方法，该方法能够更准确地定位涡旋奇点，尤其是涡旋线在三维空间的拐点。此外，通过探讨涡旋线在独立拓扑结构外的结构特性，分析了这种特殊结构的拓扑保持能力，证明了该特殊光场中拓扑演化的鲁棒性。该成果有望促进结构光场在微观尺度上的应用，以及新型超小型物理场的构造，其内在的拓扑保持演化特性可能会在拓扑结构领域的光学信息处理中展现出应用潜力。

论文链接：

https://onlinelibrary.wiley.com/doi/10.1002/lpor.201900366

{{item.product_sn}}

{{item.category_name}}