在光学科研之路的探索上，想必“以人名命名”的专业术语早已是咱们论文中的常客了。也许你早已知道这些术语背后的原理，但他们背后的光学巨匠，以及他们“留名”光学史的故事，你或许鲜有了解。在成像领域，尤其是显微成像领域，早在数百年前，我们就经历了光学人的“群星闪耀时”。16世纪发明的显微镜，在19世纪制造工艺的进步下，迎来了一个新的鼎盛期，分辨率与放大倍数不断刷新纪录。这让当时的显微镜制造商们陷入了一个认知局限，即提高制造工艺和新的设计结构才是改进显微镜性能的主要途径。但大家很快发现，一味地提高放大倍率并不能提高对细节的分辨能力。为此，19世纪迎来了一场对分辨率极限的探索，在这场探索中，三个人名留下了影响至今的印记。

“皇家天文学家”发现“艾里斑”

要知道如何判断分辨率极限，我们必然逃不开“艾里斑”，而提到“艾里斑”，就不得不聊命名的源头，19世纪的英国天文学家乔治·比德尔·艾里。

图1 乔治·比德尔·艾里 / 格林威治皇家博物馆

乔治·比德尔·艾里作为一名出色的皇家天文学家和数学家，在光学领域同样颇有造诣。而他开启光学衍射研究的初衷也很有趣：因其本人患有严重的散光，所以他设计并研磨了首个用于矫正散光的柱面透镜眼镜。

正是在研究使用圆柱透镜来校正散光现象之际，艾里进一步考察了点光源的衍射现象。

图2 艾里斑与艾里图案的二维与三维表示 / Leica

艾丽发现，点光源通过理想透镜成像时，由于衍射会在焦点处形成光斑。中央是明亮的圆斑（占84%光强），周围有一组较弱的明暗相间的同心环状条纹（占16%光强）。其中以第一暗环为界限的中央亮斑，就是日后冠以他姓名的艾里斑。

图3 《论圆孔物镜的衍射》节选 /  剑桥哲学学会会刊

当时波动说正占据上风，艾里作为波粒大战中坚定的“波动派”，选择了从衍射方向来解释，着手开始进行这一现象的数学计算。在艾里发布的著名论文《论圆孔物镜的衍射》中，就给出了该衍射图案的核心积分公式和数值解。经由后世的简化，才有了教科书上的经典公式：

sinθ≈1.22λ/d

其中，sinθ代表了艾里斑的角半径，λ为光线波长，d为圆形孔径的直径。
正是因为艾里斑的发现，告诉了全世界科学家，任何具备圆形孔径的光学仪器，都无法避免将点光源变成一个亮斑和同心圆环，分辨率存在一个“无法超越”的物理极限。
意外的是，艾里斑理论的提出，甚至成为证伪地心说的最终论据之一。

图4 托勒密地心说下恒星大小比例 / Wiki

在那个时代，利用小型望远镜观察到的恒星往往呈现圆盘形状，但这并非其真实的大小，大多是由于衍射和湍流导致的环状艾里图案。也就是说这些恒星与地球间的视差要远远大于我们的认知，间接推翻了地心说理论。

虽然艾里证明了分辨率物理极限的存在，但如何量化这一极限，艾里依旧并没有给到一个计算方案，直到另外两位光学巨头的的出现，其中之一就是蔡司公司的“天之骄子”，恩斯特·阿贝。

“光设巨头”撞到“阿贝极限”

说到显微镜，就不得不提到蔡司公司。自19世纪中叶以来，蔡司生产了当时精度最高的一批显微镜。但与当时的一众制造商一样，他们都是在用“试错法”改进显微镜性能，往往解决了一个缺陷，又会新增一个缺陷。如此低效的研发模式对于创始人卡尔·蔡司来说，是不能接受的。

为此，卡尔·蔡司决定将目光看向学术界，利用数学计算方法来改进显微系统的研发流程，他聘请了一位耶拿大学的年轻讲师作为独立研究员，这位讲师正是恩斯特·阿贝。
阿贝这个令光学人如雷贯耳的名字，在不少光学术语的命名中都有出现，诸如衡量色散的阿贝数、光学镜头设计的重要成像关系式阿贝正弦条件，以及经典的光学玻璃坐标图阿贝图等，都是他在蔡司工作期间提出的。

图5 恩斯特·阿贝 / Zeiss

作为推动光学显微镜飞速发展的先驱，阿贝很快就发现，哪怕打磨出来的镜片再完美，像差再小，标本的成像依旧会由许多重叠的且存在衍射极限的点（艾里斑）组成，也就是说显微镜的分辨率总是会达到一个极限。

为了定义这个极限，阿贝根据衍射理论推导出，两个被照亮的物体只有在相距大于光波长一半的距离时才能被分辨。

也就是说，由于衍射极限的影响，人们无法突破对特征尺寸小于二分之一波长的物体进行观测与表征。具体公式如下：

d = λ/2n*sinα = λ /(2*NA)

在这一公式中，阿贝引入了数值孔径NA这一参数，NA=n*sinα。n为物镜与标本之间介质的折射率，α为物镜能够收集到的光线的半孔径角。

d为最小的可分辨特征尺寸（分辨率），λ为照明光波长。由此可以得出，提高NA值，或者采用更短的波长，都能提高显微镜的分辨率。不过可见光波长以及数值孔径都有极限，所以常规的光学显微系统，都存在一个分辨率极限。

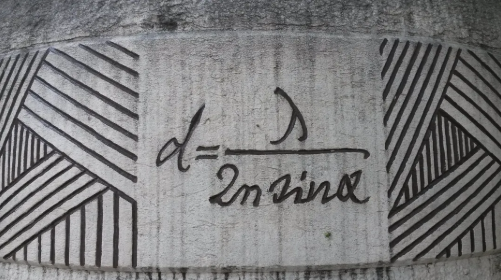图6 刻在阿贝纪念碑上的阿贝极限公式 / Wikiwand

正是由于阿贝极限的提出，人们知道了显微镜的光学性能是可以被设计和预测的，同时也终结了显微镜行业一味比拼放大倍数的“盲目内卷”。

尽管如此，实际的光学显微系统分辨率，还是靠人眼或探测器来定义的。换句话所，两个艾里斑之间，怎样才算正好可以分辨，仍没有被定义。而这个实用标准，则由英国的第三代瑞利男爵约翰·威廉·斯特拉特提出。

“高产男爵”提出“瑞利判据”

说到最高产的物理学家，第三代瑞利男爵绝对能排上名号。这位前剑桥大学校长，生涯中一共撰写了466篇论文，研究范围涵盖声学、光学、流体力学等，更是因为在1895年发现氩这一元素而荣获诺贝尔奖。以他命名的瑞利奖章依然是声学领域最高的荣誉之一。

图7 第三代瑞利男爵 / Wiki

但对于我们光学人而言，最熟悉的还是“瑞利判据”这一经典理论。瑞利男爵在艾里和阿贝的理论上做了进一步的延伸，同时考虑到了显微成像系统中聚光镜对数值孔径造成的影响。

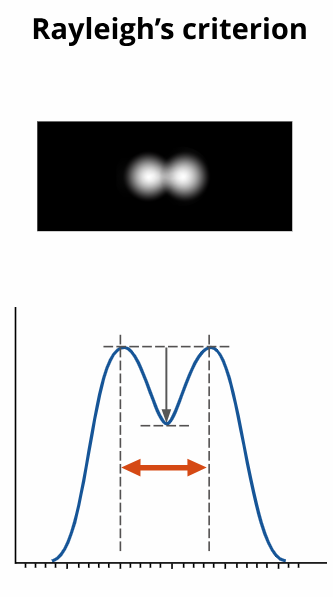图8 瑞利判据 / Myscope

瑞利判据的定义是：当一个点源的艾里斑的中心正好落在另一个点源艾里斑的第一个暗环上时，这两个点源被判定为“恰好可以分辨”。其分辨率极限公式如下：

R= 1.22 λ/NAobj+NAcond

其中λ为照明光波长，NAobj为物镜的数值孔径，NAcond为聚光镜的数值孔径。

假设我们使用最短的可见光波长，即400nm的绿光作为照明光源，并使用高NA的油浸物镜（NAobj可以达到1.5），聚光镜NA最高值约为0.95，我们通过计算可得出其分辨率约为203nm。正是因为瑞利判据的提出，常规认知中的光学显微镜水平分辨率极限，也被定义在200nm左右。

相较之下，阿贝极限更多指的是光学系统的基本极限，而瑞利判据更多是保证了实际使用中可用的对比度和分离度。所以在设计光学系统时，要想做到分辨率和图像质量之间的平衡，必须综合考量阿贝极限和瑞利判据。

打破极限

尽管三位光学先驱为显微分辨率的极限奠定了理论基础，寻求打破这一极限的探索一直没有停止。有的转向了电子显微镜，利用电子波长比可见光波长短的特性，实现了0.2nm的分辨率，放大倍数更是可以做到数百万倍，远超传统的光学显微镜。

但电子显微镜本身因为电子束容易对活细胞造成侵入性伤害，所以很难用于活体样本的检测，进一步限制了其在医疗领域的使用。为此，光学显微镜的拥护者们找到了超分辨率方法，来突破分辨率极限。

图8 因超分辨率荧光显微镜获得2014诺贝尔化学奖的三位科学家 / 诺贝尔

可以看出，我们在科研中遇到的诸多前人界定的极限，很多都只是受限于当时科研条件下得出的结论，并非不可逾越的绝对界限。随着理论进步、技术更新、材料与方法革新，任何界限都有可能被重新定义与突破。